W24 Homework 2
AM 147: Computational Methods and Applications
Due Date: January 30th, 2024
Note: Please submit your Homework as a single .zip file named:
YourlastnameYourfirstnameHW2.zip
Please strictly follow the capital and small letter formatting in the filename of the .zip file you submit. You may not receive full credit if you do not follow the file-naming conventions. Your .zip file should contain all .m files (MATLAB scripts) for the questions below.
Your .zip file must be uploaded by 11:59 PM Pacific Time on the due date. The uploads in CANVAS are time-stamped, so please plan accordingly.
In this course, all codes and computations are numerical, as opposed to symbolic computa-tion. Please do not use symbolic or any other toolbox.
Exercise 1. Sum of some entries (20 points)
Consider the outer product X := xx⊺ , x ∈ Rn , where R n denotes the set of all n × 1 vectors with real entries. Without using any loops (such as for, while, if else), we want to write a MATLAB function named SumOuterProduct.m that takes an arbitrary vector x ∈ R n as input and outputs the scalar s, equal to the sum of all entries on or above the main diagonal of the matrix X.
Write a MATLAB executable file YourlastnameYourfirstnameHW2p1.m for a random vec-tor x ∈ R 100 to compute s as follows.
close all; clear; clc
x = rand(100,1);
s = SumOuterProduct(x);
The file YourlastnameYourfirstnameHW2p1.m should have exactly the above three lines and nothing else. Please make sure to keep both the .m files in the same folder/directory so that the executable file can "see" the function it calls. Submit both .m files.
Hint: For your MATLAB function file, use the command sum (look it up in MATLAB documentation) and basic arithmetic operations such as addition (+), multiplication (*), power (.ˆ). You will not need any built-in commands other than these.
Exercise 2. A function and its approximations (30 points)
Consider 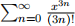 , that is, the power series obtained by keeping every third term in the Taylor expansion of exp(x). This power series corresponds to the true function
, that is, the power series obtained by keeping every third term in the Taylor expansion of exp(x). This power series corresponds to the true function
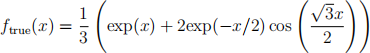
For any possible integer k, define the k term power series approximation fapprox(x, k) := 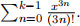
Submit a MATLAB code (.m file) named YourlastnameYourfirstnameHW2p2.m that plots 2D line plots for the functions ftrue (in black solid line) versus x ∈ [−5, 5] (in the horizontal axis). In the same figure window, plot fapprox(x, k) for k = 2 (in red dashed line), k = 3 (in green dashed line), k = 4 (in blue dashed line).
We shared a starter code YourlastnameYourfirstnameHW2p2.m inside the the CANVAS File section Files/MATLAB Files/Homework 2. You only need to complete lines 11 and 20 in that starter code, then rename the file appropriately with your first and last names.
Hint: Look up sqrt, exp, cos, sum, factorial and power (.ˆ) in MATLAB documen-tation. Also, intuition suggests that as k increases, fapprox should get closer to ftrue.