Problem Set 5
Econ 141 Fall 2023
Due on Monday, November 13th. Problem Sets should be uploaded on Gradescope before 11:59pm.
1. You are using data collected from 545 men who worked every year between 1980 and 1987. The included variables are as follows:
variable description
id person identi er
year 1980 to 1987
lwage log(wage)
le log(labor mkt experience)
black Dummy, =1 if black
hisp Dummy, =1 if Hispanic
married Dummy, =1 if married
educ years of schooling
union Dummy, =1 if worked belongs to a union
d81 Dummy, =1 if year = 1981
d82 etc
...
d87
In what follows we will assume that the error terms in our regressions are homoskedastic (recall that the Hausman test that we saw in class is valid only when the homoskedasticity assumption holds). Here we want to study the relation between log(wage), education, and experience, controlling for some other variables. We assume that the true regression is
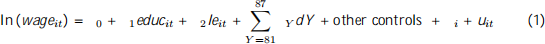
where i is the unobserved xed e ect. Note that the model includes year-speci c dummies.
(a) The sample includes data from 1980 to 1987, but equation (1) includes only dummies for years 1981 to 1987. Why?
(b) Before dealing with panel data, we have typically assumed that observations are i.i.d. . You know that independent observations are uncorrelated, so, if you can show that two observations are correlated, you showed that they cannot be independent, and then they cannot be i.i.d.. Here the error term for worker i in year t is vit = i + uit , while in year s the error is vis = i + uis . Assume that both the xed e ect i and the other error component uis have zero expected value, and you can assume that cov (uit,ujs) = 0 for every i,j,t,s (unless, of course, i = j and t = s !!). Assume also that the xed e ects are uncorrelated with all the u’s. Calculate cov (vit,vis). Is it equal to zero? Do you think that in a panel data the assumption that observations are i.i.d. is a good one?
You estimate equation (1) using RE (Random E ects), and FE (Fixed E ects) and you get the following results (standard errors are shown to the right of the corresponding coe cient):
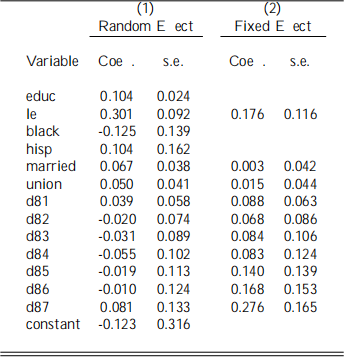
(c) Using the RE results in column (1), interpret the coe cient related to the variables educ and le.
(d) Using again RE, you run a test for the joint signi cance of all the year-speci c dummies, and the F -test is equal to 1.576. What do you conclude?
(e) Now you turn to the estimates obtained estimating equation (1) using FE (Fixed E ects). How do you justify the fact that the FE estimator did not estimate the coe cients for educ, black, and hisp?
(f) The estimated coe cients using FE and RE look quite di erent, so you suspect that the
xed e ect might be correlated with one or more included regressors. Therefore, you decide to run a Hausman test and the result is 17.2 Do you reject the null using a 5% signi cance level? And what about using a 10% signi cance level? What does the result of the test suggest about the presence of correlation between the xed e ect i and the included regressors? Based on the result of the Hausman test, is there evidence that the RE estimators are not consistent? (Note for the calculation of the number of degrees of freedom: this test is based on the comparison of coe cients estimated by using FE and RE, so you can only compare coe cients that are estimated in both models!).
2. Empirical exercise to be solved with R, Stata, etc. You want to study the relation between murder rates and death penalty. You can nd the dataset murder.xls on the Course Website. The dataset contains data from all US States for 1987, 1990, and 1993. Again, you should assume that the error terms in these regressions are homoskedastic. Make sure to include your codes and output with your homework!
(a) Estimate the following model using random e ects:
mrdrteit = 0 + 1 execit + 1 D90t + 2 D93t + i + uit. (1)
where mit is the murder rate (murders per 10,000 people) in year t and state i, execit is the number of executions in year t and during the two previous years, D90t isa dummy equal to one if t = 1990 (and D93t is analogously de ned), and i is an unobserved state- speci c, time-invariant xed e ect (the variable id in the dataset is a numerical state ID, which you will want to use instead of state when you estimate this RE model).
(b) The model does not contain a dummy equal to one if t = 1987. Why?
(c) You observe that, in the data, the unemployment rate in the state is positively correlated with the number of executions, and you suspect that unemployment may be related to murder rates. Re-estimate the model using again random e ects, but including also a measure of unemployment. The new model is then the following:
mrdrteit = 0 + 1 execit + 2 unempit + 1 D90t + 2 D93t + i + uit (2)
where unempit is the unemployment rate in state i at time t. How does 1 change when you include unempit in the regression? Explain the change in terms of omitted variable bias.
(d) In the two regressions, can you reject the null hypothesis that the predicted e ect on the murder rate of the number of executions is zero, using a 10% signi cance level?
(e) You suspect that the xed e ect i may be correlated with the regressors. Re-estimate
model (2) using fixed effects.
(f) Using FE results, calculate a 95% con dence interval for the expected e ecton the murder rate of increasing the number of executions by 30.
(g) Using FE results, test the null hypothesis that the year xed e ects are both equal to zero. Can you reject the null using a 1% and a 5% signi cance level? What does the result tell you about the change in the murder rate in the US over time, during the period 1987-93?
(h) Now you want to test the null hypothesis that the two year xed e ects are identical. You know that Cov (ˆ1 , ˆ2) = 0.24. Calculate the p-value of the test, and brie y interpret the result (using, again, FE results).