CS1800 Discrete Structures Fall 2023 Exam1

Problem 1 [12 pts (4, 4, 4)]: Two’s complement & overflow

Consider the addition of (1111)2  and (0101)2  in a 4-bit two’s complement number system:

i  Compute the addition in binary (your output must also be 4-bits).

ii Write the decimal equivalent of the operation above. For example, you might write 5 + 3 = 8.

iii Is there an overflow in this operation? Explain why or why not in one sentence.

Problem 2 [20 pts (5 each)]: English to Logic

Express each sentence using logical operators, conditionals and quantifiers.  Provide the simplest form of the statement possible (using the least number of operators, conditionals and quantifiers). Use the variables and predicates provided.

i  There is somebody who can ride their bike backwards.

(x is a person and back(x) is the event that person x can ride their bike backwards.)

ii If any car was made in the past 10 years then it has side curtain airbags and seat belts.

(x is a car, recent(x) is the event car x was made in the past 10 years and airbag(x), belt(x) represent the corresponding feature.)

iii Everybody loves chocolate or vanilla ice cream, but nobody likes both flavors.

(x is a person and choc(x) and van(x) represent person x liking those chocolate and vanilla, respectively.)

iv All the students in the earliest recitation bring a coffee to recitation, and no other student brings a coffee to recitation.

(x is a student, early(x) represents that student x is in the earliest recitation and coffee(x) represents student x brings a coffee to recitation.)

Problem 3 [12 pts (2 each)]: Tarksi World

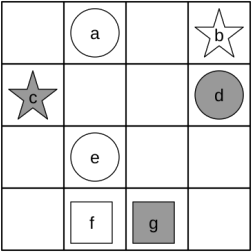
Using the following predicates:

square(x) is true if x is a square (otherwise it is false)

star(x) is true if x is a star (otherwise it is false)

circ(x) is true if x is a circle (otherwise it is false)

shade(x) is true if x is shaded (otherwise it is false)

next to(x, y) is true if x and y are adjacent horizontally, vertically or diagonally. No object is next to itself.

For each of the statements below, determine whether the statement is true or false.  You need not justify your response.

i  star(c) V 一shade(c)

ii 二x circ(x) V shade(x)

iii  Ax shade(x) Λ 一shade(x)

iv  Ax square(x) 一 一shade(x)

v AxAg(star(x) V 一shade(x) Vnext to(x, g)) 一 (shade(g) V circ(g))

vi A y 二x shade(x) Vnext to(x,y)

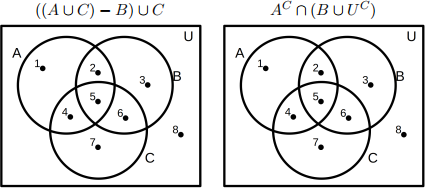
Problem 4 [12 pts (6 each)]: Set Operations

In increasing order, list all the numbered items which belong to each set.  For example, if the given set were A one could correctly respond with [1, 2, 4, 5].

i  ((A n C) — B) n C

ii  AC U (B n UC)