Physics 307 Project 7, Part 1
Part 1 due before class Wednesday, 8 November
The capstone project for this course is to create a computer model of a guitar string, then use it to study phenomena that real strings demonstrate but that aren’t typically studied in PHY360 or any other physics class.
We’re going to model the guitar string as a series of point masses (called “nodes”) that are connected by springs that follow Hooke’s law, holding the two point masses on the ends fixed. By increasing the number of these masses, we can simulate a flexible, elastic object like a guitar string and then study its properties.
We’re going to build up to this in several parts. I’m going to post the whole project as soon as possible so you can work at your own pace, but am a bit behind on posting this because of a family emergency.
1 Part 1: Hooke’s Law Forces (due before class 8 Novem-ber)
1.1 Background
Ultimately we will have many masses, but this week you can start with two fixed masses and one in the middle that can move, then increase this to two fixed and two movable masses.
(Then you will extend things to N masses.)
Your simulation will have the following properties:
• Each node has a mass m
• Each spring has a spring constant k
• Each spring has an unstretched (equilibrium) length r0
Hooke’s law says that if a spring runs between two points 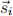 and
and 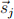 , then the force it applies to the point ri has a magnitude
, then the force it applies to the point ri has a magnitude
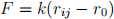
where rij is the magnitude of the separation vector given by
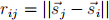
We also need the distance of this force. If rij is greater than r0 (the spring is being stretched), then the force on point 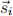 points from
points from 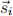 to
to 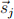 . We can describe its direction with a unit vector:
. We can describe its direction with a unit vector:

We can put these pieces together to write the force vector as a proper vector:

1.2 Assignment
1. Write code to simulate a system with three nodes: two masses that are fixed in place (perhaps at locations (0,0) and (2,0)) and one movable mass that’s free to move con-nected by springs to the two fixed masses. Your code should allow you to easily change k and r0 and to put the movable mass anywhere you like as an initial condition.
2. Play with your code and verify that it works as expected. Submit a screenshot of the animation with your report. (Note that shift-P takes a screenshot in anim – this won’t work on Macs, though.)
3. Now, extend your code to use arrays for the positions and velocities of the three masses. In Python, this will entail using a two-dimensional array; in C, this will be an array of vectors. We will talk about how to do this Friday.
4. Extend your code to two movable masses (four total). This means, for instance:
• Mass 0 is fixed and doesn’t move
• Mass 1 feels forces from mass 0 on its left and mass 2 on its right
• Mass 2 feels forces from mass 1 on its left and mass 3 on its right
• Mass 3 is fixed and doesn’t move
Submit a screenshot of this in your report.
5. In your report, discuss how you might extend this system to N total masses, where N might be dozens or hundreds. (This is the next thing you’ll do.)