DSCI 552 Machine Learning for Data Science

DSCI 552

1.  Assume that in a regression problem with one independent variable ˆ(y) = β(ˆ)0  + β(ˆ)1 x where the sample size n is 20 and the Pearson correlation r between X and Y is 0.46, Test at α = 0.01 the null hypothesis H0  : β1  = 0 vs. H1  : β1  0.

Note: Contrary to what you might think, you DO NOT need at-table for this problem or any other information.  Everything you need to solve this problem is given in this exam, please DO NOT double-check.

2.  Consider the following logistic regression problem with two classes Y = 1 and Y = 2 and one feature:

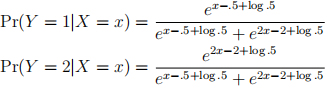
Find an LDA classiier that yields the same decision boundary as the above logistic regression problem. Assume that π1  = π2  = 0.5. It is sufficient to ind the mean of the feature in each class (i.e. μ 1  and μ2 ) and the common variance of the feature in those two classes, σ1  = σ2  = σ .

3.  Consider the following text classiication problem:

Document1: This movie is sad. It made me cry.  (Negative class)

Document 2: Cry cry cry! What a sad sad movie.  (Negative class)

Document 3: I love it!  (Positive class)

Document 4: Love this movie. Love everything about it.  (Positive class)

Dropping the stop words, the combined document (dictionary) for the above corpus has the following words: movie, sad, made, cry, love.

(a)  Create TF  (term frequency) features for each of the documents.  Do NOT use IDF (Inverse Document Frequency).

(b) Apply 1-nearest neighbor classiier with Euclidean to this dataset to classify the document “Love this sad movie.”Remember that‘’this”is a stop word and should not be used to calculate the features for this test document.

4.  For the following data set for classiication:

Assume that we want to  construct  a  regularized  logistic  regression  model  for  this dataset.

(a) Write down the L2-regularized loss function J(β0 ; β1 ) for this dataset with regu- larization parameter λ = 1.

(b)  Compare the bias variance of the regularized model with the unregularized model (λ = 0).

5.  Consider the following data set for regression:

(a)  Show all possible bootstrap samples of the dataset that have the same size as this dataset.  Note that permutations of the same data set are considered the same dataset, for example {1, 2, 3} and {2, 3, 1} are the same dataset., in which 1,2,3 are indices of the data points.

(b)  Construct  a  KNN  regression  model for  all bootstrap  samples in part  5a that contain the data point (x, y) = (0, 1) with K = 2 and predict the label for the test point x*  = 0 by averaging the predictions of those bootstrap models.