CSE 468T Introduction to Quantum Computing
Spring 2024
Exam I
Given: 6 March 2024
Due: In GradesScope by 22 March 2024, 9 AM CDT
1. (11 points) For the true/false questions below, indicate your response by marking an x in the appropriate box, like this: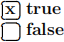 
or 
.
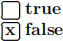Remember that ≡ means equal up to a global phase. Boldface gates are the usual Pauli gates, and H is the Hadamard gate.
• X |0> = H |−>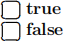 
• For k > 0, CNOTk (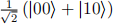 
) is an entangled state if and only if k is odd.
• After a qubit has been measured, it cannot be subjected to subsequent unitary gates.
• All superpositions of two qubits are entangled states.
• XYZZY ≡ YZ
• The state obtained after measuring the left qubit of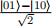 
is an entangled state.
• The i present in the Y gate can be factored out as a global phase.
• The i present in the Y gate can be factored out as a global phase for the controlled-Y gate that you developed in homework.
• At the end of teleportation, Alice tells Bob that she measured |11i for her two qubits. Which of the following gates will by itself recover Alice’s original state? (circle only one gate, or leave blank if none of the listed gates will work)
Gate X Gate Y Gate Z
• For each scenario below, what is the most precise (and true) statement you can make about |ψi ’s location on the Bloch sphere?
– |ψi is more likely to yield |0i than |1i .
– |ψi is equally likely to measure |0i as |1i .
2. (20 points) Alice and Bob prepare to participate in one of the many schemes studied this semester in which they begin with the usual Bell (also called an EPR) state:
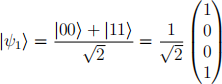
When they separate, Alice takes the left qubit and Bob takes the right qubit. They each then measure their qubit in a basis as described below.
(a) (4 points) Suppose they each measure |ψ1i in the computational (Z) basis. Which measurement outcomes are possible for this state?
(b) (4 points) In class it was shown that
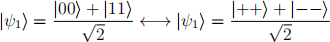
by showing the associated column vectors are mathematically equal:
The Matlab file is bellstate2ways.txt.
After separation, Alice and Bob each measure their qubit of |ψ1i in the X basis, each using a magical X-basis measuring device.
Which measurement outcomes are possible?
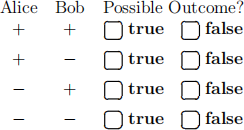
(c) (12 points) This time, due to miscommunication, Alice measures her qubit in the X basis but Bob measures his in the computational basis. This is modeled by applying the unitary gate H ⊗ I to the state 
. In other words,
Alice applies H to her qubit while Bob does nothing to his. Fill in the matrix below:
The state resulting from that operation is:
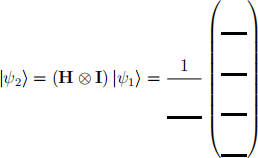
Alice and Bob each measure their qubit of |ψ2i in the computational basis. Which of the following measurement outcomes are possible?
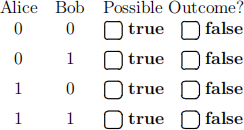
After that measurement, they reapply H ⊗ I to the measured outcome.
In which of the following states could the quantum system be now?
3. (20 points) In class we saw that if Alice and Bob each take a qubit of 
, then if they each apply gate U (limited to real values in class) to their respective qubits, the resulting state is still . This means that if they each apply the same gate U to their separate but entangled qubits, they will measure the same results consistently. The Matlab script bellstatepersists.txt from class is posted on piazza for this exam.
In this problem we look at another of Bell’s states, namely
Alice takes the left qubit and Bob takes the right qubit, as usual.
(a) (4 points) When measuring |ψ1i , Alice and Bob expect to see opposite outcomes. Specifically, basis state |01i means that if Alice sees a then Bob sees a . Similarly, basis state |10i means that if Alice sees a then Bob sees a .
(b) (5 points) Referring to state |ψ1i above, the minus sign between the two basis vectors is important for this problem, but doesn’t change the expectations from measurement, because:
• The amplitude on |01i is and its magnitude squared is .
• The amplitude on |10i is and its magnitude squared is .
• The amplitude on basis states |00i and |11i are each .
(c) (4 points) In bellstatepersists.txt we define the gate
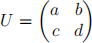
with a, b, c, d all real-valued, to make matters simple. You can keep those values real for the rest of this problem as well.
With Matlab as your (perhaps recent) faithful friend, complete the equation below to show what happens if Alice and Bob each apply U (as defined above) to |ψ1i (be sure to represent the sign on |10i properly for |ψ1i ):
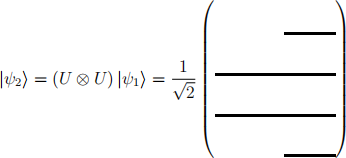
(d) (6 points) Here is a useful fact (mention this in passing at your next social gathering):
If U is unitary then |det(U)| = 1
That is, the determinant of a unitary matrix has magnitude 1.
Equipped with, aware of, and fascinated by that useful fact, prove that
In other words, Alice and Bob can apply U to this other Bell state |ψ1i and they still have (up to a global phase) state |ψ1i .
Your proof below:
(e) (1 points) If Alice and Bob begin in state |ψ1i , does that entanglement follow them into |ψ2i , after any unitary U is applied to each qubit, so that their measurements consistently and perfectly disagree?