EECE7204

Problem Set 2

Problem 1 (2.7). A noisy resistor produces a voltage vn(t). At t = t1, the noise level X = vn(t1) is known to be a Gaussian RV with pdf

Compute and plot the probability that |X| > kσ for k = 1, 2, . . ..

Problem 2 (2.17). The time-to-failure in months, X, of light bulbs produced at two manufacturing plants A and B obey, respectively, the following CDFs

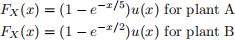
Plant B produces three times as many bulbs as plant A. The bulbs, indistinguishable to the eye, are intermingled and sold. What is the probability that a bulb purchased at random will burn at least (a) two months; (b) five months; (c) seven months?

Problem 3 (2.18). Show that the conditioned distribution of X given the event A = {b < X ≤ a} is

Problem 4 (2.22). Consider the joint pdf of X and Y :

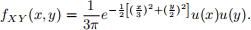
Are X and Y independent RVs? Compute the probability of {0 < X ≤ 3, 0 < Y ≤ 2}.

Problem 5 (2.27). The arrival time of a professor to his office is a continuous RV uniformly distributed over the hour between 8 a.m. and 9 a.m. Define the events:

A = {The prof. has not arrived by 8.30 a.m.}

B = {The prof. will arrive by 8:31 a.m.}

Find (a) P{B|A} and (b) P{A|B}.

Problem 6 (2.37). We are given the following joint pdf for random variables X and Y :

(a) What is the value of the constant A?

(b) What is the marginal density fX(x)?

(c) Are X and Y independent? Why?

(d) What is the conditional density fY |X(y|x)?

Figure P6 (2.37) : Support of fXY (x, y).