Economics 101 - Winter 2023
TRUE OR FALSE QUESTIONS
Mark (a) if true or (b) if false in the Scantron form.
1) In a static game, a mixed strategy for a player is a probability distribution over the actions that the player may choose.
(a) True. (b) False.
2) Every game has at least one mixed strategy Nash equilibria where at least one player is randomizing between choices (that is, choosing probabilities that are more than zero and less than one).
(a) True. (b) False.
3) The indifference principle means that a player will only choose to play two actions with strictly positive probability if that player is indifferent between those two actions, given the strategy chosen by the other players in the game.
(a) True. (b) False.
4) Every game has exactly one Nash equilibrium, which is either a pure-strategy NE or a mixed strategy NE.
(a) True. (b) False.
5) Game trees can be used to represent finite dynamic games.
(a) True. (b) False.
6) In a dynamic game, the total number of possible strategies for each player is equal to the number of periods in the game.
(a) True. (b) False.
7) In finite dynamic games, we can use backward induction to find the subgame-perfect Nash equilibria (SPNE) of the game.
(a) True. (b) False.
8) In dynamic games, we focus on SPNE, rather than regular Nash equilibria, because we want to rule out equilibria where agents act against their own interests in some subgames (that is, we want to rule out non-credible threats).
(a) True. (b) False.
9) In the SPNE of the Stackelberg model of competition seen in class (linear demand, identical marginal costs, no fixed costs), the first firm chooses a larger quantity than the second firm.
(a) True. (b) False.
10) In the SPNE of the Stackelberg model of competition, the first firm achieves higher profits than the second because we assume that consumers have stronger preferences towards innovators.
(a) True. (b) False.
11) Even if there is only one producer in a market, in some circumstances, the threat of entry of another firm may lead that producer to change their actions. For example, in an industry where adjusting production capacity takes time, the incumbent may preemptively choose a quantity that is larger than what a regular monopolist would choose to discourage future competitors.
(a) True. (b) False.
12) In a repeated prisoner’s dilemma game that is played for three rounds, the only SPNE has firms playing the dominant strategy of the stage game in all rounds (that is, there is no cooperation).
(a) True. (b) False.
13) Infinitely repeated dynamic games may have many SPNE.
(a) True. (b) False.
14) Even in an infinitely repeated prisoner’s dilemma, it is impossible to obtain cooperation, because cooperating is a strictly dominated strategy of the stage game.
(a) True. (b) False.
15) Firms will only engage in collusive agreements if they are secretly owned by the same person, or if their owners are friends. That’s because it is impossible to rationalize cooperation in an economic model where each firm only cares about their own profits.
(a) True. (b) False.
16) In a repeated game, agents place more value in future outcomes if they agents believe that the probability of the interaction happening again is high.
(a) True. (b) False.
SHORT QUESTIONS
17) Find all Nash equilibria of the following game:

(a) One pure-strategy Nash equilibrium, (U,R).
(b) One mixed-strategy Nash equilibrium, where P1 chooses U with probability 1/4 and P2 chooses L with probability 3/5.
(c) One mixed-strategy Nash equilibrium, where P1 chooses U with probability 1/3 and P2 chooses L with probability 3/4.
(d) The game has one Nash equilibria, but it is not listed above.
(e) The game has more than one Nash equilibria.
18) How many Nash equilibria of any types does the game below have? Hint: you should try to do repeated elimination of strictly dominated strategies.

(a) 0
(b) 1
(c) 2
(d) 3
(e) 4
19) Consider a market with aggregate demand Q(p) = 30 − p/4. Two firms produce homogenous goods with identical cost curves C(q) = 20q. They maximize their own profits in a dynamic game. In the first round, firm 1 chooses a non-negative price p1. In the second round, firm 2 observes firm 1’s choice and chooses their own price p2. Then, profits are determined in the style of Bertrand: consumers buy only from the lowest-price firm, and if both choose the same price, each gets half of the aggregate demand. The game is NOT repeated. Assuming firms act as prescribed in the SPNE of the game, which of the following statements is correct?
(a) Firm 1 achieves higher profits than firm 2 because it has the first-mover advantage.
(b) Firm 2 achieves higher profits than firm 1 because it has more information.
(c) Both firms achieve equal, but positive profits, because the dynamic nature of the game allows them to extract rents from consumers.
(d) Both firms achieve zero profits, as they would in a static Bertrand model.
(e) None of the options above is correct.
20) For this and the following question, consider the dynamic game below. The names P1 or P2 over the black nodes denote which of the two players makes each choice. The letters on the branches—A, B, C, D, E, F—represent actions.
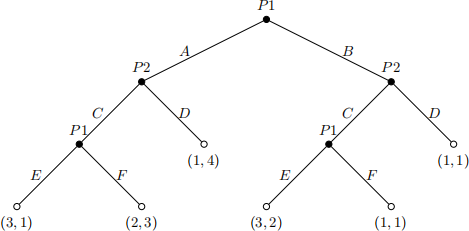
Which of the options below is an example of a possible pure strategy for player 2? Hint: It does NOT have to be the optimal strategy; this question is about what constitutes an strategy in a dynamic game.
(a) Play A.
(b) Play C.
(c) Play C if P1 chooses A, or D if P1 chooses B.
(d) Play C if P1 chooses E, or D if P1 chooses F.
(e) None of the options above is correct.
21) What is the payoff for both players in the SPNE of this game?
(a) (1,1)
(b) (3,2)
(c) (1,4)
(d) (2,3)
(e) This game has no SPNE.
22) For this and the following question, consider the stage game below. Assume that player P1 has a discount factor δ1 ∈ [0, 1), and player P2 has a potentially different discount factor δ2 ∈ [0, 1).
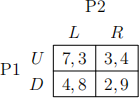
If this game is repeated three times, what is the highest payoff that Player 1 can get for the whole game, among all possible SPNE of the repeated game?
(a) 3 · (1 + δ1 + δ1 2 )
(b) 4 · (1 + δ1 + δ1 2 )
(c) 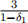
(d) 4 + 3 · 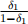
(e) None of the answers above.
23) If the stage game above is now repeated an infinite amount of times, what is the requirement on δ1—the discount factor for Player 1—such that we can have a SPNE of this game where the players play (D, L) in every round of the equilibrium path?
(a) Any δ1 ∈ [0, 1)
(b) δ1 ≥ 1/4
(c) δ1 ≥ 1/2
(d) δ1 ≥ 3/4
(e) δ1 = 2
LONG QUESTION
Consider a dynamic game of perfect information with three players. The first is a Policymaker (P ol) who makes regulatory decisions in a market. The second player is the Incumbent firm (Inc), who operates in this market no matter what. The third player is the Follower firm (F ol), who may choose to enter the market by paying a fixed cost of 2.
Both firms have constant marginal costs specified in the table below. They depend on whether firms decide to use “clean” or “dirty” technologies:

Clean technologies do not generate pollution, but have higher marginal cost. Note that the Follower is more efficient, as it has lower marginal costs than the Incumbent when using the same technology.
The timing of the game is as follows:
In the first stage, the Policymaker chooses either: NR: Do not implement any environmental regulation; or RE: Require that the Follower firm use clean technologies. The incumbent is allowed to use the dirty technology in both cases.
In the second stage, the Incumbent observes the regulatory choice from the first stage, and then chooses a monetary payment x ≥ 0 to the Policymaker. That payment can be zero.
In the third stage, the Follower observes the previous regulatory and payment deci-sions, and then decides whether to enter (FE) or not (FN).
After those choices are made and observed, the firms operating in the market simul-taneously decide their price and which production technology to use, subject to the regulatory constraints. If the Follower has not entered, the Incumbent is as a monop-olist. If the Follower entered, competition is Bertrand: consumers only buy from the firm offering the lowest price, and if they post the same price, aggregate demand is evenly split between them. Aggregate demand is Q(p) = 10 − p.
The Policymaker’s payoff is:

where p* is the equilibrium price in the market, Q∗ is the aggregate consumption, QD is the total number of units which were produced using the “dirty” technology, and x is the payment chosen by the Incumbent. That is, the Policymaker values consumer surplus, would like to avoid pollution, but also likes the payment.
The payoff for the Incumbent is the profits they get minus the payment x made to the Policymaker.
The payoff for the Follower is zero if it does not enter, and its profits if it enters the market (including the fixed cost of 2).
24) Which of the following game trees best describe this game, up to the entry choice of the follower? Note: alternatives (d) and (e) are not used in this question.
(a) 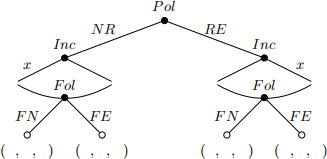
(b) 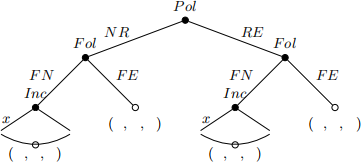
(c) 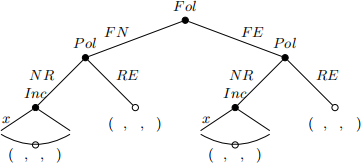
(d) Not used in this question.
(e) Not used in this question.
25) What is a pure strategy for the Follower firm?
(a) A decision to regulate the market, RE
(b) An optimal choice of payment to the Policymaker, x.
(c) Whether to enter as a function of the previous payment x.
(d) For every combination of regulatory decision (NR or RE) and payment by the Incumbent (x), a decision of whether to enter (F E) or not enter (F N).
(e) A choice of whether to regulate or not as a function of the payment x.
26) Refer to the game tree you chose on Question 24. Consider the endings (hollow circles) following the choice of whether to enter or not by the Follower. For each of those end-ings, note the resulting market structure (monopoly or Bertrand? ). Next, write what are the marginal costs of each firm operating, based on previous regulatory decisions (hint: a firm will only use clean technologies if required by regulations). Use that to calculate the profits of the Follower in each ending (remember the fixed cost). Based on that calculation, what do you think is the optimal strategy for the Follower?
(a) Enter (F E) in all circumstances.
(b) To make a payment of x = 6 to the regulator.
(c) Not Enter (F N) in all circumstances.
(d) Make a payment of x = 6 and Not Enter (F N).
(e) Enter (F E) in all histories where there is no environmental regulation (NR); and Not Enter (F N) in all histories where there is environmental regulation for new firms (RE).
27) Suppose that, before the start of the game, the Incumbent firm promises to make a sizable payment to the Policymaker if they choose to create environmental regulations for new firms only (RE). Basing your analysis on the concept of subgame-perfect Nash equilibria, how do you think the Policymaker would react?
(a) The Policymaker would find the promise credible and it could affect their regula-tory decision, if the payment were large enough.
(b) The Policymaker would NOT find the promise credible, because after the regula-tion choice is made, the Incumbent would have no incentives to keep its promise as it would only reduce the Incumbent’s payoff.
(c) The Policymaker would NOT find the promise credible, because the RE regulation hurts the Incumbent’s profits.
(d) The Policymaker would respond with a counter-offer proposing a higher x, starting a bargaining game.
(e) The Policymaker would ask if the Incumbent has funding secured.
28) Based on the optimal choices of the Follower (from question 26) and the Incumbent (from question 27), evaluate the payoffs the Policymaker should expect depending on their regulatory choice. Hint: with demand Q(p) = 10 − p, a monopolist with marginal cost 4 would choose quantity q m = 3, leading to price p m = 7.
(a) The Policymaker’s payoff is strictly higher with no environmental regulation.
(b) The Policymaker’s payoff is strictly higher with environmental regulation for new firms.
(c) The Policymaker is indifferent between NR and RE.
(d) It is impossible to know because the Incumbent is indifferent between at least two values of x, and thus the Policymaker cannot predict the Incumbent’s behavior.
(e) It is impossible to know because the Follower is indifferent between entering and not entering, and thus the Policymaker cannot predict the Follower’s behavior.
29) Now suppose that the Policymaker has a third regulatory option: to require clean technologies of all firms, instead of only new entrants (call it RA). The rest of the game proceeds as previously described. Calculate the expected payoff of this new regulation for the Policymaker, as you did in the previous question. Does that change your conclusions?
(a) No; the regulation that was best in the previous question is still the best.
(b) Yes; environmental regulation for all firms yields a higher payoff to the regulator.
(c) The Policymaker is indifferent between RA and another regulatory option.
(d) It is impossible to know because the Incumbent is indifferent between at least two values of x, and thus the Policymaker cannot predict the Incumbent’s behavior.
(e) It is impossible to know because the Follower is indifferent between entering and not entering, and thus the Policymaker cannot predict the Follower’s behavior.