Please read these instructions carefully!

This assignment counts for 20% of your final module mark. The maximum score for this coursework is 50 marks. As before you are expected to produce a report in R Markdown and then submit is as a pdf file. Note that you should not use the RStudio viewer to print the file to pdf!!! Instead knit your .Rmd file and then you will find the pdf file is produced in the same directory in which the .Rmd file is located. This is the file that you should upload. The penalty for late submission of the pdf file is a zero mark.

Your report should be of a professional standard. Imagine you are producing work for a client. It should be presentable and understandable by someone who is familiar with linear models. It is not enough to provide material from which an intelligent person could construct a solution! Instead it is your responsibility to explain your results clearly, correctly and concisely. Make sure to justify your conclusions appropriately. Your answers should be given in full sentences and be relevant to the question. Numerical output should be appropriately rounded and presented in sentences and not as raw R output. Graphs should be of an appropriate size, have clear axes labels (including units of measurement, if appropriate) and legends or captions. 5 marks are allocated for the overall presentation style of the report.

You are also expected to submit the R Markdown file that you used to produce your report. If you do not submit the R Markdown file or the file submitted does not compile into the report that you have submitted, your total mark will be reduced by 5 marks. To ensure the file can be compiled into the report, only use R packages that were introduced in the computer practicals or have been listed as permitted on the discussion forum. If you struggle to compile your report on your personal computer, a cloud version of RStudio is available via moodle in the section Computer Practicals.

Do not include R code in your report! If you include R code in your report, your total mark will be reduced by up to 5 marks. Handwritten answers will not be awarded marks.

Deliverable	Comment	Penalty
Report	must be a pdf file	late submission: 0 marks
	R code included in report	up to 5 marks penalty
	handwritten answer	0 marks for answer
.Rmd file	must compile into submitted report	late/no submission 5 marks penalty
	use only packages from computer practicals/lectures or listed as permitted on the discussion forum

Make sure you read the questions carefully. If you have any queries about the coursework, please post them on the ST231 forum, but do not post any part of your solutions. You can also submit questions to the anonymous question form on moodle.

Please ensure that you submit in good time before the deadline. Please read Chapter 5 in the course guide which gives details around the procedures regarding coursework including applying for extensions and lateness penalties. If you have submitted the wrong file, please contact the UG support office, not the module leader. Submissions via e-mail are not accepted.

Please be aware that your work will be submitted to TurnItIn, a piece of plagiarism-detection software. Cases of suspected collusion or plagiarism will be followed up as outlined in Section 5.3 of the course guide. Note that detailed discussions of the assignment or comparisons of numerical/graphical results or computer code are not permitted. Furthermore the use of AI such as ChatGBT or other generative artificial intelligence tools are not permitted.

Good luck with the assignment!

Instructions

Download the file dia2.csv from moodle and save it to your working directory. Make sure your R markdown file is located in the same directory and that you have declared the directory to R as your working directory using the top toolbar commands Session > Set Working Directory > Choose Directory.... Then load the data into R using a relative file path, that is a command like dia <- read.csv("dia2.csv").

The dataset consists of information on 400 round diamonds.1 The variables are:

• price: the price of the diamond in US Dollars;

• width: the width of the diamond in mm;

• clarity: the clarity rating of the diamond, which is one of

Fit the following model to the data:

Model 1: log(price) ≥ width + clarity

Question 1 - Unusual observations [Total 30 marks]

Overall presentation [3 marks]

(a) [2 marks] What type of variable is clarity? What data structure is used in R to accommodate such a variable?

(b) [6 marks] For a simple linear regression model (with an intercept term) the relationship between the values of the predictor variable and the leverages is given by

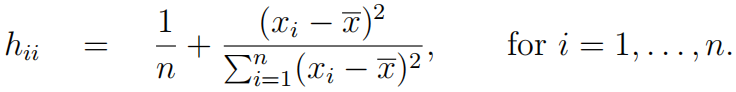
Present a plot that illustrates the relationship between the leverages of the observations and the values of the predictor variables for Model 1. Explain what the plot reveals about the relationship.

(c) [2 marks] For Model 1, identify any observations that are regression outliers, that is, any observations that have an absolute standardised residual larger than 3. Report the indices of these observations as well as their standardised residual.

(d) [8 marks] Produce a residuals versus leverage plot for Model 1 using different colours/symbols for the four levels of clarity. Taking into account what you have discovered in (b), comment on the plot. Also discuss what the plot tells us about the observations identified in (c).

(e) [2 marks] Present the Cook’s distances of the observations identified in (c) and compare them to the rule of thumb threshold introduced in the lectures. What do you conclude?

(f) [3 marks] Remove the observation with the largest absolute standardised residual from the dataset and fit Model 1 again. Present a table that illustrates how the removal of the regression outlier affects the estimated coefficients. What do you conclude?

(g) [4 marks] For this sub-question the term outlier refers to the regression outlier that was removed in (f). The variable clarity splits the data into four groups and Model 1 fits a regression line for each group. In the following you are asked to explore graphically the effect it has on Model 1 when we remove the outlier. For each group in the full dataset, produce a scatterplot of price against width. Furthermore, in each scatterplot, illustrate the effect that removing the outlier has on the fitted regression curve for that group. Indicate the observation that is the outlier in the relevant scatterplot. Briefly comment on the plots.

Question 2 - Inference for Model 1 [Total 20 marks]

Overall presentation [2 marks]

Below is the R model summary output for Model 1.

Call:

lm(formula = log(price) ~ width + clarity, data = dia)

Residuals:

Min 1Q Median 3Q Max

-0.50945 -0.14158 0.00013 0.15015 1.61367

Coefficients:

Estimate Std. Error t value Pr(>|t|)

(Intercept) 1.02797 0.09393 10.94 <2e-16 ***

width 1.06700 0.01550 68.86 <2e-16 ***

clarityVS1 0.76968 0.03162 24.34 <2e-16 ***

clarityVVS1 0.98182 0.03863 25.42 <2e-16 ***

clarityIF 1.10449 0.04935 22.38 <2e-16 ***

---

Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 0.214 on 395 degrees of freedom

Multiple R-squared: 0.9261, Adjusted R-squared: 0.9253

F-statistic: 1237 on 4 and 395 DF, p-value: < 2.2e-16

(a) [2 marks] Predict the price (in US Dollars) for a diamond that has a clarity rating I1 and a width of 5.5 mm. Explain how this can be computed from the information provided in the model summary above.

(b) [3 marks] Give a quantitative interpretation of the estimated coefficient for clarityIF with respect to price (in US Dollars).

(c) [7 marks] The row for clarityVS1 reports on a hypothesis test. Assuming a 5% significance level, explain which hypothesis test is performed and how the result should be interpreted. Make sure to clearly state

(d) [2 marks] Explain how an unbiased estimate for the error variance ‡2 can be derived from the model summary output and report the estimate.

(e) [4 marks] Consider an internally flawless diamond with a width of 5.34 mm. In R compute a 95% prediction interval for the log-price of such a diamond and report the interval. Explain how to derive from this a 95% prediction interval for the price of this diamond. Report the 95% prediction interval for the price of this diamond.