EC420: Introduction to Econometric Methods - Spring 2024
Problem Set 2. Due on Monday, February 12th, at 10AM. Please upload it in D2L.
Please show your work in detail.
Theory
1. Wooldridge Chapter 2, Problem 1
Let kids denote the number if children ever born to a woman, and let educ denote years of education for the woman. A simple model relating fertility to years of education is:
kids = β0 + β1educ + u
where u is the unobserved error.
(a) What kinds of factors are contained in u? Are these likely to be correlated with level of education?
(b) Will a simple regression analysis uncover the ceteris paribus effect of education on fer-tility? Explain.
2. Wooldridge Chapter 2, Problem 2
In the simple linear regression model y = β0 + β1x + u, suppose that E(u) ≠ 0. Letting α0 = E(u), show that the model can always be rewritten with the same slope, but a new intercept and error, where the new error has a zero expected value.
3. Wooldridge Chapter 2, Problem 4 parts (i), (ii) and (iii) only. (7th Edition)
The data set BWGHT.RAW contains data on births to women in the United States. Two variables of interest are the dependent variable, infant birth weight in ounces (bwght), and an explanatory variable, average number of cigarettes the mother smoked per day during pregnancy (cigs). The following simple regression was estimated using data on n = 1, 388 births:
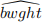= 119.77 − 0.514cigs
(a) What is the predicted birth weight when cigs = 0? What about when cigs = 20 (one pack per day)? Comment on the difference.
(b) Does this simple regression necessarily capture a causal relationship between the child’s birth weight and the mother’s smoking habits? Explain.
(c) To predict a birth weight of 125 ounces, what would cigs have to be? Comment.
Applied
1. Wooldridge Chapter 2, Computer Exercise C1.
The data in 401K.RAW are a subset of data analyzed by Papke (1995) to study the rela-tionship between participation in a 401(k) pension plan and the generosity of the plan. The variable prate is the percentage of eligible workers with an active account; this is the variable we would like to explain. The measure of generosity is the plan match rate, mrate. This variable gives the average amount the firm contributes to each worker’s plan for each $1 con-tribution by the worker. For example, if mrate = 0.50, then a $1 contribution by the worker is matched by a 50¢ contribution by the firm.
(a) Find the average participation rate and the average match rate in the sample of plans.
(b) Now, estimate the simple regression equation
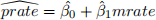
and report the results along with the sample size and R-squared.
(c) Interpret the intercept in your equation. Interpret the coefficient on mrate.
(d) Find the predicted prate when mrate = 3.5. Is this a reasonable prediction? Explain what is happening here.
(e) How much of the variation in prate is explained by mrate? Is this a lot in your opinion?
(f) Test the null hypothesis that β1 ≤ 0 against the alternative that β1 > 0 using a t-test with significance level of 5%. What is the p-value of your test? How does your choice of critical value depend on whether you can assume the population is normally distributed? Compute a 90% non-rejection region (confidence interval) for your test. See the lecture notes on Angel for details on how to compute a non-rejection region for a one-sided test.
2. Wooldridge Chapter 2, Computer Exercise C4 (7th Edition)
Use the data in WAGE2.RAW to estimate a simple regression explaining monthly salary (wage) in terms of IQ score (IQ).
(a) Find the average salary and average IQ in the sample. What is the sample standard deviation of IQ? (IQ scores are standardized so that the average in the population is 100 with a standard deviation equal to 15.)
(b) Estimate a simple regression model where a one-point increase in IQ changes wage by a constant dollar amount. Use this model to find the predicted increase in wage for an increase in IQ of 15 points. Does IQ explain most of the variation in wage?
(c) Now, estimate a model where each one-point increase in IQ has the same percentage effect on wage. If IQ increases by 15 points, what is the approximate percentage increase in predicted wage?
3. Wooldridge Chapter 2, Computer Exercise C6 (7th Edition)
We used the data in MEAP93.RAW for Example 2.12. Now we want to explore the relation-ship between the math pass rate (math10) and spending per student (expend).
(a) Do you think each additional dollar spent has the same effect on the pass rate, or does a diminishing effect seem more appropriate? Explain.
(b) In the population model
math10 = β0 + β1log(expend) + u
argue that β1/10 is the percentage point change in math10 given a 10% increase in expend.
(c) Use the data in MEAP93.RAW to estimate the model from part (ii). Report the esti-mated equation in the usual way, including the sample size and R-squared.
(d) How big is the estimated spending effect? Namely, if spending increases by 10%, what is the estimated percentage point increase in math10?
(e) One might worry that regression analysis can produce fitted values for math10 that are greater than 100. Why is this not much of a worry in this data set?