STAT2004J – Linear Modelling
Tutorial 4

Question 1. Given that , show that R2 is the same as the square of the sample correlation between

(a) X and Y

(b) Y and 

(c) Verify these relationships using the following data:

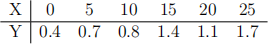
Question 2. The hardness H of a porcelain enamel depends on the temperature of curing T. In a controlled experiment the following data were collected:

(a) Plots these data - does a simple regression model seem appropriate?

(b) Fit the simple regression model and construct the ANOVA tables using the corrected total sums of squares.

(c) Fit the model

E(y) = β0

and calculate the residual sum of squares.

Question 3. Suppose that random variables Y1, ..., Yn are independently and Normally distributed with common variance σ2 and expectations of the form

E(Yi) = β0 + β1Xi    (i = 1, ..., n),

where σ, β0, β1 are unknown parameters and the Xi ’s are known values of an explanatory variable.

(a) Show that the joint probability density function of Y1, ..., Yn is

where

(b) Show that the maximum likelihood estimates of β0 and β1 are the same as their least squares estimates. Also find the maximum likelihood estimate of σ2.