COMP9021 Principles of Programming
Term 1, 2024
Assignment 2
Worth 13marks and due Week 11 Monday @ 10am
1. General Matters
1.1 Aim
The purpose of this assignment is to design and implement a program that will:
. analyse the various characteristics of a maze, represented by a particular coding of its basic constituents into numbers stored in a file whose contents is read, and
. either display those characteristics, or
. output some Latex code in a file, from which a pictorial representation of the maze can be produced.
. use object-oriented programming.
1.2 Marking
This assignment is worth 13 marks distributed approximately as follows:
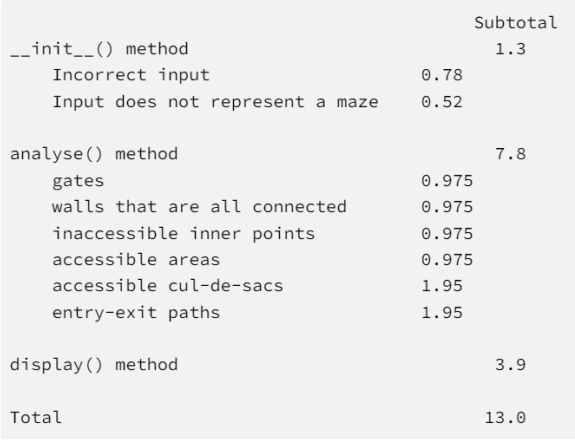
Your program will be tested against several inputs. For each test, the automarking script will let your program run for 30 seconds. The outputs of your program should be exactly as indicated.
1.3 Due Date and Submission
Your program will be stored in a file named maze.py. The assignment can be submitted more than once. The last version just before the due date and time will be marked (unless you submit late in which case the last late version will be marked).
Assignment 2 is due Week 11 Monday 22 April 2024 @ 10:00am (Sydney time)
Note that late submission with 5% penalty per day is allowed up to 5 days from the due date, that is, any late submission after Week 11 Saturday 27 April 2024 @ 10:00am will be discarded.
Make sure not to change the filename maze.py while submitting by clicking on [Mark] button in Ed. It is your responsibility to check that your submission did go through properly using Submissions link in Ed otherwise your mark will be zero for Assignment 2.
Please note that the testing is done in two steps. You can test part 1 of the assignment in “Assignment 2: for testing of part 1 and for submission” on the sample inputs.
Your submission will NOT be downloaded from “Assignment 2: NOT for submission, for testing of part 2 ONLY” for marking. You can ONLY test part 2 of the assignment in “Assignment 2: NOT for submission, for testing of part 2 ONLY” on the sample inputs.
Please also note that your submission for BOTH PART 1 AND PART 2 will be downloaded from “Assignment 2: for testing of part 1 and for submission” for marking.
1.4 Reminder on Plagiarism Policy
You are permitted, indeed encouraged, to discuss ways to solve the assignment with other people.
Such discussions must be in terms of algorithms, not code. But you must implement the solution on your own. Submissions are scanned for similarities that occur when students copy and modify other people’s work or work very closely together on a single implementation. Severe penalties apply.
2. Description
The representation of the maze is based on a coding with the four digits 0, 1, 2 and 3 such that:
. 0 codes points that are connected to neither their right nor below neighbours
. 1 codes points that are connected to their right neighbours but not to their below ones: 
. 2 codes points that are connected to their below neighbours but not to their right ones: 
. 3 codes points that are connected to both their right and below neighbours: 
A point that is connected to none of their left, right, above, and below neighbours represents a
pillar: 
Analysing the maze will allow you to also represent:
. cul-de-sacs: 
. certain kinds of paths: 
3. Examples
3.1 First example
The file named maze_1.txt has the following contents:
1 0 2 2 1 2 3 0
3 2 2 1 2 0 2 2
3 0 1 1 3 1 0 0
2 0 3 0 0 1 2 0
3 2 2 0 1 2 3 2
1 0 0 1 1 0 0 0
Here is a possible interaction:
$ python3
...
>>> from maze import *
>>> maze = Maze('maze_1.txt')
>>> maze.analyse()
The maze has 12 gates.
The maze has 8 sets of walls that are all connected.
The maze has 2 inaccessible inner points.
The maze has 4 accessible areas.
The maze has 3 sets of accessible cul-de-sacs that are all connected.
The maze has a unique entry-exit path with no intersection not to cul-de-sacs. >>> maze.display()
The effect of executing maze.display() is to produce a file named maze_1.tex that can be given asargument to pdflatex to produce a file named maze_1.pdf that views as follows.

3.2 Second example
The file named maze_2.txt has the following contents.
022302120222
222223111032
301322130302
312322232330
001000100000
Here is a possible interaction:
$ python3
...
>>> from maze import *
>>> maze = Maze('maze_2.txt')
>>> maze.analyse()
The maze has 20 gates.
The maze has 4 sets of walls that are all connected.
The maze has 4 inaccessible inner points.
The maze has 13 accessible areas.
The maze has 11 sets of accessible cul-de-sacs that are all connected.
The maze has 5 entry-exit paths with no intersections not to cul-de-sacs. >>> maze.display()
The effect of executing maze.display() is to produce a file named maze_2.tex that can be given asargument to pdflatex to produce a file named maze_2.pdf that views as follows.

3.3 Third example
The file named labyrinth.txt has the following contents.
31111111132
21122131202
33023022112
20310213122
31011120202
21230230112
30223031302
03122121212
22203110322
22110311002
11111101110
Here is a possible interaction:
$ python3
...
>>> from maze import *
>>> maze = Maze('labyrinth.txt')
>>> maze.analyse()
The maze has 2
gates.
The maze has 2 sets of walls that are all connected.
The maze has no inaccessible inner point.
The maze has a unique accessible area.
The maze has 8 sets of accessible cul-de-sacs that are all connected.
The maze has a unique entry-exit path with no intersection not to cul-de-sacs. >>> maze.display()
The effect of executing maze.display() is to produce a file named labyrinth.tex that can be given as argument to pdflatex to produce a file named labyrinth.pdf that views as follows.

4. Detailed description
4.1 Input
The input is expected to consist of ydim lines of xdim members of {0, 1, 2, 3}, where xdim and ydim are at least equal to 2 and at most equal to 31 and 41, respectively, with possibly lines consisting of spaces only that will be ignored and with possibly spaces anywhere on the lines with digits. If n is the xth digit of the yth line with digits, with 0 ≤ x < xdim and 0 ≤ y < ydim , then
. n is to be associated with a point situated x ×0.5 cm to the right and y ×0.5 cm below an origin,
. n is to be connected to the point 0.5 cm to its right just in case n = 1 or n = 3, and
. n is to be connected to the point 0.5 cm below itself just in case n = 2 or n = 3.
The last digit on every line with digits cannot be equal to 1 or 3, and the digits on the last line with digits cannot be equal to 2 or 3, which ensures that the input encodes a maze, that is, a grid of width (xdim - 1) × 0.5 cm and of height (ydim - 1) × 0.5 cm (hence of maximum width 15 cm and of maximum height 20 cm), with possibly gaps on the sides and inside. A point not connected to any of its neighbours is thought of as a pillar; a point connected to at least one of its neighbours is thought of as part of a wall.
We talk about inner point to refer to a point that lies (x + 0.5) × 0.5 cm to the right of and (y + 0.5) × 0.5
cm below the origin with 0 ≤ x < xdim − 1 and 0 ≤ y < ydim − 1.
4.2 Output
Consider executing from the Python prompt the statement from maze import * followed by the state- ment maze = Maze(some_filename). In case some_filename does not exist in the working directory, then Python will raise a FileNotFoundError exception, that does not need to be caught. Assume that some_filename does exist (in the working directory). If the input is incorrect in that it does not contain only digits in {0, 1, 2, 3} besides spaces, or in that it contains either too few or too many nonblank lines,or in that some nonblank lines contain too many or too few digits, or in that two of its nonblank lines do not contain the same number of digits, then the effect of executing maze = Maze(some_filename) should be to generate a MazeError exception that reads
Traceback (most recent call last):
...
maze.MazeError: Incorrect input.
If the previous conditions hold but the further conditions spelled out above for the input to qualify as a maze (that is, the condition on the last digit on every line with digits and the condition on the digits on the last line) do not hold, then the effect of executing maze = Maze(some_filename) should be to generate a MazeError exception that reads
Traceback (most recent call last):
...
maze. MazeError: Input does not represent a maze.
If the input is correct and represents a maze, then executing maze = Maze(some_filename) should have the effect of outputting a first line that reads one of
The maze has no gate.
The maze has a single gate.
The maze has N gates.
with N an appropriate integer at least equal to 2, a second line that reads one of
The maze has no wall.
The maze has walls that are all connected.
The maze has N sets of walls that are all connected.
with N an appropriate integer at least equal to 2, a third line that reads one of
The maze has no inaccessible inner point.
The maze has a unique inaccessible inner
point.The maze has N inaccessible inner points.
with N an appropriate integer at least equal to 2, a fourth line that reads one of
The maze has no accessible area.
The maze has a unique accessible
area.
The maze has N accessible areas.
with N an appropriate integer at least equal to 2, a fifth line that reads one of
The maze has no accessible cul-de-sac.
The maze has accessible cul-de-sacs that are all connected.
The maze has N sets of accessible cul-de-sacs that are all connected.
with N an appropriate integer at least equal to 2, and a sixth line that reads one of
The maze has no entry-exit path with no intersection not to cul-de-sacs.
The maze has a unique entry-exit path with no intersection not to cul-de-sacs. The maze has N entry-exit paths with no intersections not to cul-de-sacs.
with N an appropriate integer at least equal to 2.
. Agate is any pair of consecutive points on one of the four sides of the maze that are not connected.
. An inaccessible inner point is an inner point that cannot be reached from any gate.
. An accessible area is a maximal set of inner points that can all be accessed from the same gate (sothe number of accessible inner points is at most equal to the number of gates).
. A set of accessible cul-de-sacs that are all connected is a maximal setS of connected inner points that can all be accessed from the same gate g and such that for all points p in S, if p has been accessed from g for the first time, then either p is in a dead end or moving on without ever gettingback leads into a dead end.
. An entry-exit path with no intersections not to cul-de-sacs is a maximal setS of connected inner points that go from a gate to another (necessarily different) gate and such that for all points p in S, there is only one way to move on from p without getting back and without entering a cul-de- sac.
Pay attention to the expected format, including spaces.
If the input is correct and represents a maze, then executing maze = Maze(some_filename) followed by maze.display() should have the effect of producing a file named some_filename.tex that can be givenas argument to pdflatex to generate a file named some_filename.pdf. The provided examples will show you what some_filename.tex should contain.
. Walls are drawn in blue. There is a command for every longest segment that is part of a wall. Horizontal segments are drawn starting with the topmost leftmost segment and finishing with the bottommost rightmost segment. Then vertical segments are drawn starting with the topmostleftmost segment and finishing with the bottommost rightmost segment.
. Pillars are drawn as green circles.
. Inner points in accessible cul-de-sacs are drawn as red crosses.
. The paths with no intersection not to cul-de-sacs are drawn as dashed yellow lines. There is a command for every longest segment on such a path. Horizontal segments are drawn starting with the topmost leftmost segment and finishing with the bottommost rightmost segment, with thosesegments that end at a gate sticking out by 0.25 cm. Then vertical segments are drawn starting with the topmost leftmost segment and finishing with the bottommost rightmost segment, with those segments that end at a gate sticking out by 0.25 cm.
Pay attention to the expected format, including spaces and blank lines. Lines that start with % are
comments; there are 4 such lines, that must be present even when there is no item to be displayed of the kind described by the comment. The output of your program redirected to a file will be compared with the expected output saved in a file (of a different name of course) using the diff command. For
your program to pass the associated test, diff should silently exit, which requires that the contents of both files be absolutely identical, character for character, including spaces and blank lines. Check your program on the provided examples using the associated .tex files, renaming them as they have the names of the files expected to be generated by your program.