Math 466
Spring 2024
Assignment 9
1. Consider the linear input output system:
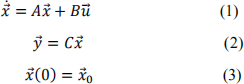
where![]() ∈ Rn,
∈ Rn, ![]() ∈ Rp , and
∈ Rp , and ![]() ∈ Rm. It is desired to input signals of the form
∈ Rm. It is desired to input signals of the form ![]() = −K
= −K![]() +
+ ![]() where the
where the
feedback term −K![]() serves to stabilize the system so that resonance can be averted. The term
serves to stabilize the system so that resonance can be averted. The term ![]() represents an external disturbance or forcing function. Unfortunately, however, we are unable to measure the entire state,
represents an external disturbance or forcing function. Unfortunately, however, we are unable to measure the entire state, ![]() , and can only observe
, and can only observe ![]() as given by the output equation
as given by the output equation ![]() = C
= C![]() . To remedy this, we design an
. To remedy this, we design an
observer system the state of which approximates ![]() . We then input a signal of the form
. We then input a signal of the form

and attempt to design the feedback gain Kin such away that we obtain the desired result. The observer system takes the form
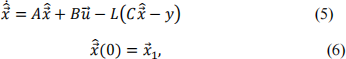
where the matrix L is an appropriately chosen gain.
a. What are the dimensions of the design matrices Kand L?
b. Let ![]() =
= ![]() −
− ![]() , and use (1)-(3), (5),(6) to show that
, and use (1)-(3), (5),(6) to show that ![]() satisfies the homogeneous linear system given by
satisfies the homogeneous linear system given by
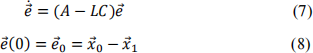
c. Give a design condition on the gain L that will guarantee that lim ![]() (t) = 0 (and therefore that t→∞
(t) = 0 (and therefore that t→∞
t(l)![]()
![]() (t) −
(t) − ![]() (t)) = 0.
(t)) = 0.
d. Now substitute the input given by (4) with ![]() (t) = 0(⃗⃗) into (1) and (5) and use (1)-(8) to find a 2n
(t) = 0(⃗⃗) into (1) and (5) and use (1)-(8) to find a 2n
dimensional first order homogeneous linear system describing the evolution of the 2n
dimensional vector function given by

e. Give a design condition on the gain K, that when used in conjunction with the design criteria
given in part (c) will guarantee that lim ![]() (t) = 0 and therefore the design objective has been met. t→∞
(t) = 0 and therefore the design objective has been met. t→∞
(Hint: For a block upper triangular matrix of the form T = [ 0(u) v(w)] , it follows that
det T = detudetv . If you do not see how this hint is helpful, then you may have made an error in parts ((a) –(d)).
f. In the case of the undamped simple harmonic oscillator with both mass and stiffness set equal to one (i.e. m = k = 1) and the ability to measure only displacement and not velocity, provide
explicit conditions on the elements in the gains L and kthat will ensure that the conditions you set out in parts (c) and (e) are satisfied.
g. Use Simulink to demonstrate that your design in part (f) works by choosing values for the gains L and kthat satisfy the conditions you set out in part (f) for the cases (i) v(t) = 0, and (ii) v(t) = sint.
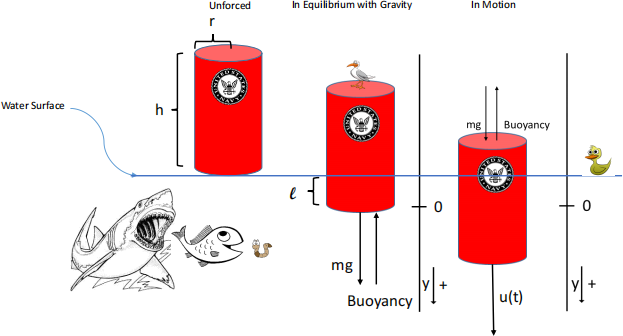
2. A United States Navy Contractor is designing the next generation of sono-buoy. A sono-buoy
is a device used to track enemy submarines. It is dropped into the ocean from low flying aircraft and sends out low frequency sound waves which travel through the water and bounce off of large metallic objects such as a submarine. The new generation of sono-buoy is cylindrical in shape
with circular bases and floats on the surface of the ocean with the circular bases at the top and
bottom. See the figure on the next page. The radius of the circular bases is rand the height of the cylinder ish. The average mass density of the sono-buoy isp and the mass density of seawater is pw.
a. What is the mass m of the sono-buoy in terms of p,T, and ℎ.
b. The buoyancy (which is a force!) of an object is equal in magnitude to the weight of water being displaced. In terms of l, at equilibrium with gravity, what is the buoyancy?
c. Based on part (b), what must lbe equal to?
d. In order to be able to accurately process the data it receives from the sono-buoy, the Navy requires a mathematical model for the vertical motion of the device as it bobs up and
down on the surface of the ocean. Let u(t) denote any external forces acting on the
device at time t ≥ 0, and use Newton’s second law to derive a differential equation for the quantity measured in reference to the coordinate system shown in the figure. Write your model as a first order linear input/output system.
e. Using either Laplace transforms or the matrix exponential and the variation of constant formula, provide an expression for the output, y, in terms of the input u.
f. If incoming ocean waves aremodeled in the form of a cosine function of the form,
u(t) = R cos幼t
where 幼 is never larger than some frequency 幼max, in designing the sono-buoy, what values of the sono-buoy dimensions,h, r and p will the Navy engineers want to avoid and why?
g. If in their design, the Navy decides to include a damping device that can be modeled via a term that is proportional to the vertical velocity of the sono-buoy, with a positive constant of proportionality b, where the value of b depends on the design of the damper, how
should the damper be designed (i.e. how should the gain b be chosen) so as to achieve critical damping?
h. Choose reasonable values for p,T, and ℎ, lookup pw, and simulate your model using
Simulink for different values of R, b and 幼. In your simulations, be certain to include examples where you choose values for 幼 that cause the system response to exhibit beats and resonance. Be certain to pay careful attention to units and make conversions where necessary.
3. Why are marching soldiers told to “break step” when they cross a bridge? In this problem we will see how a
marching column of soldiers can de-stabilize a flexible bridge. Model the bridge as an undamped simple harmonic oscillator with mass m and stiffness k, assume that the bridge is initially at rest when the soldiers begin marching across it, and model the marching soldiers as a sequence of pulses or impulses. That is, set
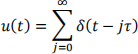
where δ(t) is the unit impulse (Dirac delta function) at time t = 0 (and therefore its translate, δ(t − c), is the unit impulse at time t = c) and τ > 0 is a constant that represents the time it takes the soldiers to take a single step. Show that for an appropriate choice of τ (that of course will depend on the values of mandk) a resonance-like situation will result and the amplitude of the oscillations of the bridge will grow without bound. (Hint: Use the impulse response function and the convolution form of the solution you found as part of Problem 3 in Assignment 4, the integration properties of the Dirac delta function, and the fact that the system being linear with zero initial conditions, implies that the response of the system to a sum of inputs, will be the sum of the responses of the system to each of the individualsummands that make up the input. Or equivalently that integration is a linear operation. It may also help to realize that u can be written as
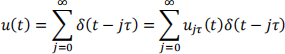
where uc (t) is the unit step function at t = c; uc (t) = 1, fort ≥ c anduc (t) = 0, fort < c .)
4. Use Simulink to simulate your results in Problem 1 for the case where a) τ is such that resonance occurs, b) τ is such that resonance does not occur, and c) the soldiers have “broken step” and are casually walking across the bridge (this last one will require your modeling skills and possibly Matlab’s random number generator! ![]() )
)