EECS 280 Project 5: Machine Learning
Winter 2024 release.
Checkpoint due 8:00pm EST Friday April 12, 2024. See Submission and Grading / Checkpoint.
Full project due 8:00pm EST Monday April 22, 2024.
You may work alone or with a partner (partnership guidelines). If you work alone, you must work alone on both the checkpoint and the full project. If you work with a partner, you must work with the same partner on the checkpoint and the full project. You may not work alone on the checkpoint and then add a partner for the full project.
Introduction
Automatically identify the subject of posts from the EECS 280 Piazza using natural language processing and machine learning techniques.
The learning goals of this project include Function Objects and Recursion. We’ll reinforce learning goals from project 4: Container ADTs, Dynamic Memory, The Big Three, Linked Lists, and Iterators. You will gain experience with recursion, binary trees, templates, comparators, and the map data structure.
For example, your program will be able to read a Piazza post like this and figure out that it’s about Project 3: Euchre.

Setup
Set up your visual debugger and version control, then submit to the autograder.
Visual debugger
During setup, name your project p5-ml . Use this starter files link:
https://eecs280staff.github.io/p5-ml/starter-files.tar.gz
VS Code Visual Studio Xcode
You should end up with a folder with starter files that look like this. You may have already renamed files like Map.hpp.starter to Map.hpp . You may also have a main.cpp file after following the setup tutorial. If not, you will create a main.cpp file in the Classifier section.
$ ls
BinarySearchTree.hpp instructor_student.out.correct
BinarySearchTree_compile_check.cpp projects_exam.out.correct
BinarySearchTree_public_tests.cpp sp16_projects_exam.csv
BinarySearchTree_tests.cpp.starter test_small.csv
Makefile test_small.out.correct
Map.hpp test_small_debug.out.correct
Map_compile_check.cpp train_small.csv
Map_public_tests.cpp unit_test_framework.hpp
Map_tests.cpp.starter w14-f15_instructor_student.csv
TreePrint.hpp w16_instructor_student.csv
csvstream.hpp w16_projects_exam.csv
Here’s a short description of each starter file.
File(s) Description
BinarySearchTree.hpp.starter Starter code for BinarySearchTree .
BinarySearchTree_tests.cpp.starter Your BinarySearchTree unit tests.
BinarySearchTree_public_tests.cpp A small test for BinarySearchTree
BinarySearchTree_compile_check.cpp Compile check test for BinarySearchTree
TreePrint.hpp Test helper function for printing trees.
Map.hpp.starter Starter code for Map.
Map_tests.cpp.starter Your Map unit tests.
Map_public_tests.cpp Your Map unit tests.
Map_compile_check.cpp Compile check test for Map .
csvstream.hpp Library for reading CSV files.
train_small.csv
test_small.csv
test_small.out.correct
test_small_debug.out.correct Sample input and output for the main program.
sp16_projects_exam.csv
w14-f15_instructor_student.csv
w16_instructor_student.csv
w16_projects_exam.csv
instructor_student.out.correct
projects_exam.out.correct Piazza data input from past terms, with correct output.
Makefile Helper commands for building.
unit_test_framework.hpp A simple unit-testing framework.
Version control
Set up version control using the Version control tutorial.
After you’re done, you should have a local repository with a “clean” status and your local repository should be connected to a remote GitHub repository.
1 $ git status
2 On branch main
3 Your branch is up-to-date with 'origin/main'.
4
5 nothing to commit, working tree clean
6 $ git remote -v
7 origin https://github.com/awdeorio/p5-ml.git (fetch)
8 origin https://githubcom/awdeorio/p5-ml.git (push)
You should have a .gitignore file (instructions).
1 $ head .gitignore
2 # This is a sample .gitignore file that's useful for C++ projects.
3 ...
Group registration
Register your partnership (or working alone) on the Autograder. Then, submit the code you have.
BinarySearchTree
A binary search tree supports efficiently storing and searching for elements.
Write implementations in BinarySearchTree.hpp for each _impl function. The file already contains function stubs and you should replace the assert(false) with your code. For example:
BinarySearchTree.hpp
1 static bool empty_impl(const Node *node) {
2 assert(false); // Replace with your code
3 }
Run the public Binary Search Tree tests.
1 $ make BinarySearchTree_compile_check.exe
2 $ make BinarySearchTree_public_tests.exe
3 $ ./BinarySearchTree_public_tests.exe
Write tests for BinarySearchTree in BinarySearchTree_tests.cpp using the Unit Test Framework. You’ll submit these tests to the autograder. See the Unit Test Grading section.
1 $ make BinarySearchTree_tests.exe
2 $ ./BinarySearchTree_tests.exe
Submit BinarySearchTree.hpp and BinarySearchTree_tests.cpp to the autograder.
Setup
Rename these files (VS Code (macOS), VS Code (Windows), Visual Studio, Xcode, CLI):
BinarySearchTree.hpp.starter -> BinarySearchTree.hpp
BinarySearchTree_tests.cpp.starter -> BinarySearchTree_tests.cpp
The BinarySearchTree tests should compile and run. The public tests and compile check will fail until you implement the functions. The test you write ( BinarySearchTree_tests.cpp ) will pass because the starter file only contains ASSERT_TRUE(true) .
1 $ make BinarySearchTree_compile_check.exe
2 $ make BinarySearchTree_public_tests.exe
3 $ ./BinarySearchTree_public_tests.exe
4 $ make BinarySearchTree_tests.exe
5 $ ./BinarySearchTree_tests.exe
Template Parameters
BinarySearchTree has two template parameters:
T - The type of elements stored within the tree.
Compare - The type of comparator object (a functor) that should be used to determine whether one element is less than another. The default type is std::less , which compares two T objects with the < operator. To compare elements in a different fashion, a custom comparator type must be specified.
No Duplicates Invariant
In the context of this project, duplicate values are NOT allowed in a BST. This does not need to be the case, but it avoids some distracting complications.
Sorting Invariant
A binary search tree is special in that the structure of the tree corresponds to a sorted ordering of elements and allows efficient searches (i.e. in logarithmic time).
Every node in a well-formed binary search tree must obey this sorting invariant:
It represents an empty tree (i.e. a null Node* ).
- OR -
The left subtree obeys the sorting invariant, and every element in the left subtree is less than the root element (i.e. this node).
- AND -
The right subtree obeys the sorting invariant, and the root element (i.e. this node) is less than every element in the right subtree.
Put briefly, go left and you’ll find smaller elements. Go right and you’ll find bigger ones. For example, the following are all well-formed sorted binary trees:
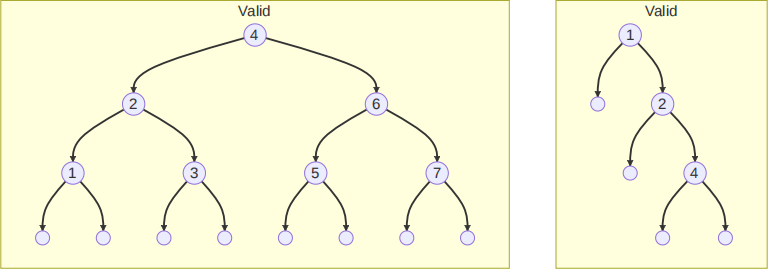
While the following are not:
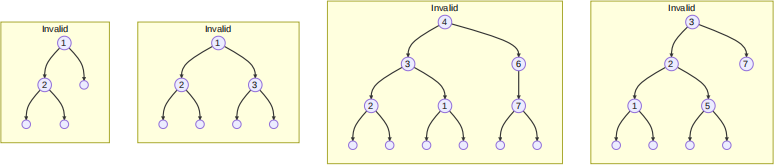
ProTip: When writing tests for check_sorting_invariant() , you can use an iterator to break the invariant. For example:
1 BinarySearchTree b;
2 b.insert(1);
3 b.insert(0);
4 // change first datum to 2, resulting in the first broken tree above
5 *b.begin() = 2;
6 ASSERT_FALSE(b.check_sorting_invariant());
Data Representation
The data representation for BinarySearchTree is a tree-like structure of nodes similar to that described in lecture. Each Node contains an element and pointers to left and right subtrees. The structure is self-similar. A null pointer indicates an empty tree. You must use this data representation. Do not add member variables to BinarySearchTree or Node .
Public Member Functions and Iterator Interface
The public member functions and iterator interface for BinarySearchTree are already implemented in the starter code. DO NOT modify the code for any of these functions. They delegate the work to private, static implementation functions, which you will write.
Implementation Functions
The core of the implementation for BinarySearchTree is a collection of private, static member functions that operate on tree-like structures of nodes. You are responsible for writing the implementation of several of these functions.
To disambiguate these implementation functions from the public interface functions, we have used names ending with _impl . (This is not strictly necessary, because the compiler can differentiate them based on the Node* parameter.)
There are a few keys to thinking about the implementation of these functions:
The functions have no idea that such a thing as the BinarySearchTree class exists, and they shouldn’t. A “tree” is not a class, but simply a tree-shaped structure of Node s. The parameter node points to the root of these nodes.
A recursive implementation depends on the idea of similar subproblems, so a “subtree” is just as much a tree as the “whole tree”. That means you shouldn’t need to think about “where you came from” in your implementation.
Every function should have a base case! Start by writing this part.
You only need to think about one “level” of recursion at a time. Avoid thinking about the contents of subtrees and take the recursive leap of faith.
We’ve structured the starter code so that the first bullet point above is actually enforced by the language. Because they are static member functions, they do not have access to a receiver object (i.e. there’s no this pointer). That means it’s actually impossible for these functions to try to do something bad with the BinarySearchTree object (e.g. trying to access the root member variable).
Instead, the implementation functions are called from the regular member functions to perform specific operations on the underlying nodes and tree structure, and are passed only a pointer to the root Node of the tree/subtree they should work with.
The empty_impl function must run in constant time. It must must be able to determine and return its result immediately, without using either iteration or recursion. The rest of the implementation functions must be recursive. There are additional requirements on the kind of recursion that must be used for some functions. See comments in the starter code for details. Iteration (i.e. using loops) is not allowed in any of the _impl functions.
Using the Comparator
The _impl functions that need to compare data take in a comparator parameter called less. Make sure to use less rather than the < operator to compare elements!
The insert_impl Function
The key to properly maintaining the sorting invariant lies in the implementation of the insert_impl function - this is essentially where the tree is built, and this function will make or break the whole ADT. Your insert_impl function should follow this procedure:
1. Handle an originally empty tree as a special case.
2. Insert the element into the appropriate place in the tree, keeping in mind the sorting invariant. You’ll need to compare elements for this, and to do so make sure to use the less comparator passed in as a parameter.
3. Use the recursive leap of faith and call insert_impl itself on the left or right subtree. Hint: You do need to use the return value of the recursive call. (Why?)
Important: When recursively inserting an item into the left or right subtree, be sure to replace the old left or right pointer of the current node with the result from the recursive call. This is essential, because in some cases the old tree structure (i.e. the nodes pointed to by the old left or right pointer) is not reused. Specifically, if the subtree is empty, the only way to get the current node to “know” about the newly allocated node is to use the pointer returned from the recursive call.
Technicality: In some cases, the tree structure may become unbalanced (i.e. too many nodes on one side of the tree, causing it to be much deeper than necessary) and prevent efficient operation for large trees. You don’t have to worry about this.