Hello, if you have any need, please feel free to consult us, this is my wechat: wx91due
MATH21112 Rings and Fields
Example Sheet 7
More on Ideals
1. Show that if R is any ring then R is a division ring if the only right ideals of R are {0} and R. (A similar statement is true for left ideals).
2. Let R = Z and let I = <3>. What is I2 ? What is In? Let J = <12>. What is IJ?
3. Let I, J be ideals of a ring R. Show that IJ ≤ I ∩ J. Give an example to show that this inclusion may be proper.
4. Let R be a commutative ring and set N(R) = {r ∈ R | ∃n ∈ N, rn = 0} to be the set of all nilpotent elements of R. Prove that N(R) is an ideal of R. Compute N(R) for:
(i) R = Z12 ;
(ii) R = Z24 ;
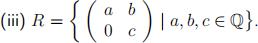
5. Suppose that I , J are ideals of the commutative ring R such that I + J = R. Prove that IJ = I ∩ J.
6. (Hard) Let p be a prime integer and set Z(p) = {n/m ∈ Q | p | n}. Prove
that Z(p) is a subring of Q. Show that the only proper non-trivial ideals of Z(p)are those generated by powers of p.