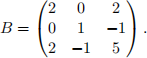Hello, if you have any need, please feel free to consult us, this is my wechat: wx91due
Lineare Algebra II
¨Ubungsblatt 10
SS 2024
Aufgabe 1. Es sei V ⊂ R[X] der Unterraum aller Polynome vom Grad ≤ 3. F¨ur f, g ∈ V definiere
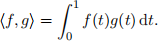
a) Zeigen Sie, dass ⟨·, ·⟩ eine symmetrische positiv definite Bilinearform auf V ist. [Hinweis: F¨ur Integration d¨urfen Sie sich frei aus der Analysis bedienen.]
b) Wenden Sie das Gram-Schmidt-Orthonormalisierungsverfahren auf die Basis {1, x, x2 , x3} von V an um eine Orthonormalbasis zu konstruieren.
Aufgabe 2. Es sei n ∈ N>0 und V = C n×n die Menge aller n × n-Matrizen mit komplexen Eintr¨agen, aufgefasst als C-Vektorraum. Definiere die Abbildung
⟨·, ·⟩: V × V → C
(A, B) 7→ Spur(¯A T B).
a) Zeigen Sie, dass ⟨·, ·⟩ eine Hermitische positiv definite Semilinearform auf V ist.
b) Es sei U ⊂ V der Unterraum bestehend aus den Diagonalmatrizen. Bestimmen Sie das orthogonale Komplement von U in V bez¨uglich ⟨·, ·⟩.
Aufgabe 3. a) Sei n ∈ N>0. Zeigen Sie, dass eine Matrix B ∈ R n×n symmetrisch und positiv definit ist genau dann wenn B = RT R f¨ur eine obere Dreiecksmatrix R ∈ R n×n mit positiven Diagonaleintr¨agen. [Hinweis: Eine Richtung wurde bereits in der Vorlesung gezeigt.]
b) Bestimmen Sie jene Werte λ ∈ R f¨ur welche die Matrix
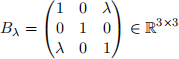
positiv definit ist. [Hinweis: Verwenden Sie a) indem Sie den Ansatz Bλ = RT R machen.]
Aufgabe 4. a) Sei n ∈ N>0 und sei B ∈ R n×n eine symmetrische positiv definite Matrix. Zeigen Sie: Es gibt genau eine Diagonalmatrix D ∈ R n×n mit positiven Diagonaleintr¨agen und genau eine obere Dreiecksmatrix L ∈ R n×n mit Einsen auf der Diagonalen, sodass
B = LT DL .
[Hinweis: Starten Sie mit einer Zerlegung der Form B = RT R wie in Aufgabe 3a).]
b) Bestimmen Sie Zerlegungen der Form B = RT R und B = L T DL f¨ur die Matrix