AMS 335/ECO 355: GAME THEORY

Hello, if you have any need, please feel free to consult us, this is my wechat: wx91due

AMS 335/ECO 355:  GAME THEORY

SUMMER 2024

FIRST EXAM

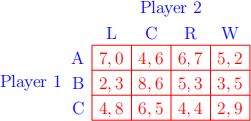
Question 2

Consider an asymmetric Cournot duopoly game, where the two firms have different costs of production.  Each firm chooses simultaneously  (and independently) how much to produce. Firm 1 selects quantity q1  at a production cost of 4q1 .  Firm 2 selects quantity q2  and pays the production cost of 2q2 . The market inverse demand is given by p = 12 − q1  − q2 .

(a) (5 points) Write down the normal form of this game.

(b) (5 points) What is the best response correspondence of each firm?

(c) (5 points) Find the pure-strategy Nash equilibrium of this game. What is the profit of each firm at the Nash-equilibrium production levels?

Question 3

Two workers at the Meta Headquarters in Menlo Park, California need to work closely on a project.  Each worker i =  1, 2 chooses simultaneously (and independently) an amount of effort ei   ≥ 0 (measured in hours of work per day) to invest on the project.  The effort is costly, but there are synergies between the two workers.  The value to each worker from effort levels (e1 , e2 ) is e1 + 2e2 + e1 e2 . Worker 1’s cost of effort is 5/1e1(2) and worker 2’s cost of effort is 2e2(2).

(a) (5 points) Write down the normal form of this game.

(b)  (5 points) What is the best response correspondence of each worker?

(c) (5 points) Find the pure-strategy Nash equilibrium of this game.

(d) (5 points) Which strategies are rationalizable for each worker?  (i.e., survive the pro- cess of iterated elimination of strategies that are not best responses for any surviving play of the opponent)

(e)  (5 point) Suppose workers choose effort levels (e1  = 11, e2  = 4).  Does this strategy profile Pareto dominate the Nash-equilibrium effort levels? Explain.

Question 4

Three students witness another student cheating in the exam.  Each of the three students would like the professor to be informed about the cheating, but prefers that somebody else reports it.  Each of the three students chooses simultaneously (and independently) whether to email the professor (strategy E) or not (strategy N). When no one sends an email, each of the three students bears a cost of -1.  If at least one student sends an email to the professor, students who email obtain a benefit of 3, and those who don’t email obtain a benefit of 5.

(a) (5 points) Write down the normal form of this game.  How many pure-strategy profiles does this game have?

(b) (5 points) What is the best response correspondence of a student to every possible combination of strategies of the other two students?

(c) (5 points) Find all pure-strategy Nash equilibria of this game.   How  many  pure- strategy Nash equilibria does this game have?

(d) (5 points) Compute a symmetric mixed-strategy Nash equilibrium (i.e., an equilib- rium in which every student emails the professor with the same probability p ∈ (0, 1)). (It is ok if you cannot solve for the exact p, as long as you can write the correct equa- tion from which you would compute the exact p.)

Question 5

Four friends just passed by an empty tennis court, so they think of playing a match.  Each of the four friends chooses simultaneously (and independently) whether they want to play (strategy P) or not (strategy N). A tennis match can only be played with  exactly two  or four players.  If the match can be played, each of the four friends gets a benefit of 4  (even those who do not participate). Every friend who wants to play bears a cost of 2 (regardless of whether the match is played or not).  A friend who doesn’t want to play bears a cost of 1.

(a) (5 points) Write down the normal form of this game.  How many pure-strategy profiles does this game have?

(b) (5 points) What is the best response correspondence of a friend to every possible combination of strategies of the other three friends?

(c) (5 points) Find all pure-strategy Nash equilibria of this game.   How  many  pure- strategy Nash equilibria does this game have?

(d) (5 points) Compute a symmetric mixed-strategy Nash equilibrium in this game in which every friend wants to play with the same probability p ∈ (0, 1).  (It is ok if you cannot solve for the exact p, as long as you can write the correct equation from which you would compute the exact p.  There could be more than one symmetric mixed-strategy Nash equilibrium.)