Hello, if you have any need, please feel free to consult us, this is my wechat: wx91due
Exam 1: ECON207, 2024 Summer
Submission Instructions
Please submit your solutions before the deadline through the blackboard the Exam 01 folder.
Late submissions will not be accepted and academic dishonesty will be punished.
On your answer sheet,write down following Honor Pledge with your signature:
“I affirm that I will not give or receive any unauthorized help on this exam,and that all work will be my own.” .
Please make sure that you must justify all your answers and show the steps you have taken. Also,when you draw graphs,please make sure to label the axis,functions,and points you specified.Missing labels will result in points losses.
Instruction for Reference
Since it is an open-book exam,I ask you to provide references for all of your steps to all of your answers(except for trivial ones).For instance,when you apply Lagrangian Erpression into a constraint optimization problem,you need to refer to one of the learning materials
you've studied.(For instance,page of your textbook or page of lecture slide)
It will take a bit of your time,but I expect that if you actually studied,you can locate where you should refer in a very short time.Thus,the purpose of this practice is to check whether your answers came from your learning.
1.Three Demand Curves
Consider a 2-good economy in which price of good x is pa and price of good y is py.
We assume that,for each x and y,marginal utility of consuming x and y are positive.
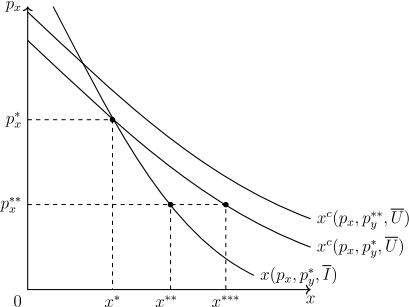
(a)Explain what positive marginal utility means with respect to a satiation point.
(b)Determine whether good x is normal or inferior good.
(c)Suppose  Determine whether good x and y are substitutes or complements.
Determine whether good x and y are substitutes or complements.
(d)Can you determine whether a normal good y is price elastic or inelastic?
(e)Compare compensation variation and change in the consumer surplus from the decrease in price of x from ps to pa*.Explain the implication.
(f)Suppose V(p*,P,I)=U₂.Can you draw a possible 
If you can,then draw a graph of x(px,P,U₂);otherwise explain why.
2. Excess Burden of Taxation
Consider 2-good economy in which a consumer has $20 to spend,prices of x and y are P=$0.5 and py=$1.The preference of the consumer is represented by
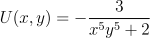
(a)Write down the consumer's budget constraint and illustrate it on a graph.
(b)Find the consumer's optimal consumption bundle.Show your answer in a graph.
(c)From what you drawn in(b),argue why only the slopes of indifference curve and budget constraint are matter in this case.
(d)Suppose that the government impose a tax of $0.5 per unit on purchases of x. Compute the tax revenues T from the consumer's new optimal consumption bundle.
(e)You may want to argue that tax scheme in(d)is harmful than the revenue T.How can you justify your argument?
(e)Can you suggest better tax scheme than(d)?You need to define what is “better” .
3. Short takes
1. Shopping
There are two stores in the town,selling two goods x and y.Store 1 sells x at $2 and y at $10.Store 2 sells x at $4 and y at $5.Since they are far from each other,visiting both store costs $20 for transportation.(*for simplicity,visiting only one store costs nothing)
Draw carefully budget constraints of a consumer with $30 and a consumer with $80.
2. Quasi-linear utility
U(x,y)=√T+y
Show that the income effect on good x is always zero.(as long as optimal consumption is an interior solution of utility maximization problem.)Relate with this result to compensating variation and equivalent variation with respect to a change in price of x.
3.Chicken and Egg
Suppose that a consumer has convex Indifference Curves and he purchased 6 units of chicken and 10 units of egg in the last week.In this week,the price of chicken goes down but the price of egg goes up.Suppose there are no change in his utility function.Budget
constraint of the last week and the this week intersect at (8,8).
Can he rationally consume 12 units of egg in this week?Justify your answer using a graph.
4.Duality and Elasticity
Consider two-good economy in which a consumer's preference is represented by U(x,y)= x°y°,where a,β>0.The consumer faces price(Pa,Py)for x and y with income of I.
(a)Show that his preference is convex,and explain why we do care.
From now on,assume a =β=1.
(b)Set a corresponding utility maximization problem as a constrained optimization problem.You need to clearly state what is objective and constraint.
Then find the demand (x(px,Py,I),y(px,Py,I))for each good (as function of pa,Py,I).
(c)Find the indirect utility function as function of pa,Py,I.
(d)Find the compensated demand(x*,yf)for each good (as function of pa,Py,I)
(Note:NOT function of pa,Py,U.Think how we can express U as a function of Px,Py,I.)
(e)Justify your answer in(d), by solving corresponding expenditure minimization problem.
(f)Suppose p=1,Py=1,I=10.Then consider a situation in which an increase in pa makes p=2.Find Price Elasticity and Compensated Price Elasticity correspond to the situation.Explain a relationship between those two elasticities.