Math 124A, Winter 2023
Midterm II (Collingwood)
February 21, 2023
1. (15 points) Find the derivatives of the following functions. Do not simplify. Your final answers must give the derivative in terms of x. Use any rules you wish. Place your final answer in the box. No work required.

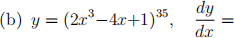
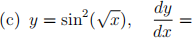

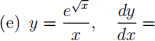
2. (4 points) Compute the slope of the tangent line to the curve y = xsin(πx) at the point where x = 3/2. Give EXACT answers.
3. (4 points) Suppose

Find ALL x so that F’ (x) = 0. (Recall, arctan(. . .) = tan−1 (. . .).)
4. (10 points) An object is moving in the plane along a curve with parametric equations
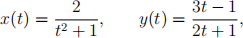
where t ≥ 0 is in units of seconds and the units on the coordinate axes are feet. Put your answers in the boxes. Some work required for each part to receive credit. Give EXACT answers or three decimal places of accuracy.
(a) (True or False) The vertical velocity at time t is always positive. Explain.
(b) At time t, what is the slope of the curve at the object location?
(c) What is the initial speed of the object (i.e. speed at time t = 0)?
(d) What is the equation of the tangent line to the path when the object crosses the x-axis?
5. (11 points) The equation
x2 − 4xy + 8y2 = 1
defines an ellipse. You must show work on each part to receive credit. Give EXACT answers.
(a) Find a formula (in terms of x and y) for the implicit derivative dx/dy .
(b) Find a point on the ellipse where the tangent line is parallel to the line x + y = 1. (There are two possible answers; either is acceptable.)
5. continued
(c) What is the slope of the tangent line to the curve at the point P = (1, 1/2)?
(d) What is the value of the second implicit derivative at the point P = (1, 1/2); i.e. 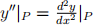 ?
?
6. (6 points) The pictured right triangle has sides y and w which are elastic and will stretch when the vertex P is pulled in the direction indicated. Assume that as P is pulled in the picture, the triangle is always a right triangle with base 3 feet. Show some work. Give EXACT answers or answers accurate to 3 decimal places.
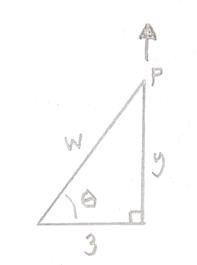
(a) Suppose y is increasing at a rate of 7 ft/sec. When y = 5 feet, what is the rate at which w is changing?
(b) Suppose θ is increasing at a rate of 0.1 rad/sec. When θ = π/3 radians, what is the rate at which w is changing?