Econ 101
Intermediate Microeconomics
Winter 2022
Practice Midterm 2
Part 1: Short questions
1. Michela and Nick are playing Katan. It’s Michela’s turn, she needs to decide between attacking the Mountain or the River. After observing Michela’s action, Nick will decide to attack back or not. The last move will be Michela’s. If Nick attacks back she can decide to revenge or retire. The payoffs are the following:
. (8,4) if Michela chooses Mountain, Nick attacks and Michela revenges.
. (6,6) if Michela chooses Mountain, Nick attacks and Michela retires.
. (10,5) if Michela chooses Mountain and Nick does not attack.
. (6,8) if Michela chooses River, Nick attacks and Michela revenges.
. (4,10) if Michela chooses River, Nick attacks and Michela retires.
. (8, 7) if Michela chooses River and Nick does not attack.
How many subgames does this game have?
(a) 10
(b) 5
(c) 8
(d) 4
(e) 16
2. Assume we are in the same game as in the previous question. Which actions are observed in thr subgame perfect Nash equilibrium (SPNE) of this game?
(a) (Mountain, Revenge, Revenge; Attack, Attack)
(b) (Mountain, Revenge, Retire; Attack, Not Attack)
(c) (Mountain, Revenge, Revenge; Not Attack, Attack)
(d) (River, Retire, Revenge; Not Attack, Not Attack)
(e) (River, Retire, Retire, Not Attack, Attack).
3. Consider the following statements about the concept of subgame perfect Nash equilib- rium (SPNE):
(I) This concept only applies to repeated games, where the same stage game is played every round.
(II) Some dynamic games might have a Nash equilibrium that is not a SPNE.
(III) The concept of SPNE rules out situations where a player would be acting against their own interest in at least one subgame of the complete dynamic game.
(a) All options are incorrect.
(b) Only I is correct.
(c) Only II is correct.
(d) Only III is correct.
(e) More than one option are correct.
4. Which of those characterize what is a strategy in a dynamic game?
(I) Each strategy corresponds to an action in a specific ”round” of the game. So for a long game, the player chooses several strategies in sequence.
(II) In a strategy, a particular choice of action can be a function of past actions of the other players, as long as those past actions are observable to others.
(III) The principle of backward induction says that the best strategy for a player is to wait until all others have made their actions before taking any actions in the game.
(a) All options are incorrect.
(b) Only I is correct.
(c) Only II is correct.
(d) Only III is correct.
(e) More than one option are correct.
5. A firm is considering inviting its main competitor to become part of a cartel. Are the questions below important, in the sense that they determine whether the cartel would be sustainable?
(I) Is it easy to observe the price that my competitor is actually charging from his clients?
(II) Do I expect my competitor and I to be in this market for a long time?
(III) Is there a way to credibly punish this other firm in case of a deviation?
(a) None of the options are important.
(b) Only II and III are important.
(c) Only I and III are important.
(d) Only I and II are important.
(e) All of the options are important.
6. Consider the following game:
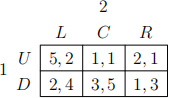
Define p the probability that player 1 plays U, q the probability that player 2 plays L, and s the probability that player 2 plays C. In a mixed strategies Nash Equilibrium these probabilities are given by:
(a) p = 1/2 and q = 2/5; s = 1/5
(b) p = 1/2 and q = 1/5; s = 0
(c) p = 1/5 and q = 2/5; s = 3/5
(d) p = 2/3 and q = 1/5; s = 0
(e) p = 1/3 and q = 2/5; s = 0
7. Two firms are repeating the following stage game 5 times. Assume there is no dis- counting. Which of the following is NOT TRUE?

(a) There is a SPNE where the two firms play (H, M) in every period
(b) The payoff (10, 10) can be achieved in the first period in a pure strategy SPNE
(c) There are two pure strategy Nash Equilibria in the stage game
(d) Even if they utilize a grim-trigger strategy, the two firms cannot achieve a better payoff than getting (3, 3) every period
(e) If the payoff to (M, L) is changed to (0, 0), then the two firms playing (H, M) in every period is the only pure strategy SPNE
8. In an infinitely repeated game, N identical firms (N ≥ 2 is finite) compete every period a la Bertrand. All firms have constant marginal costs c ≥ 0 and no fixed costs. The market demand is given by Q = a − bp, where a,b > 0. Firms are secretly considering a collusive strategy where they start by playing the monopoly price pm , and keep doing so as long as they don’t see any firm picking a different price in the past. If there is such a deviation, then all firms switch permanently to playing the price corresponding to the Nash equilibrium of the static Bertrand game.
Which of the following statements is CORRECT?
(a) If regulators impose a price ceiling 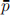 ∈ (c,pm ) in this market (that is, no firm can choose prices higher than
∈ (c,pm ) in this market (that is, no firm can choose prices higher than 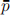 ), which implies a lower collusive price, then it becomes easier to sustain the collusive agreement.
), which implies a lower collusive price, then it becomes easier to sustain the collusive agreement.
(b) If a decreases, i.e., market demand goes down, then it becomes harder to sustain the collusive agreement.
(c) The larger the number of firms N, the easier it is to sustain the collusive agree- ment.
(d) If a price floor p ∈ (c,pm ) is imposed (that is, no firm can choose prices lower
than p), then is becomes harder to sustain the collusive agreement.
(e) None of the above is correct.
9. Suppose we want to sustain cooperation in a situation where both economic agents have short-run incentives to unilaterally deviate, but because they expect the situation to occur again in the future, they might benefit from cooperating. Think of this situation as analogous to the infinitely repeated prisoner’s dilemma. Which of the following statements is INCORRECT (if any)?
(a) The higher the perceived probability of interaction being repeated, the easier it is to sustain cooperation.
(b) The less the agents care about the future, the harder it is to sustain cooperation.
(c) The harder it is to detect a deviation, the harder it is to sustain cooperation.
(d) The higher the interest rate, the easier it is to sustain cooperation.
(e) None of the statements above are incorrect.
Part 2: Long questions
First long question 1
Consider a Cournot market where the equilibrium price is is given by p(Q) = 20 − 2Q, where Q is the aggregate quantity being produced by all firms. There are multiple potential entrepreneurs, indexed by i = 1, 2, ... , with possibly different cost curves. The items below will consider different assumptions about entry and costs.
10. Assume that there are only two entrepreneurs with cost curves C1 (q1 ) = 6q1 and C2 (q2 ) = 4q2. Entrepreneur 1 chooses quantity first and is able to credibly commit to this choice. Then entrepreneur 2 choose its quantity after observing firm 1’s quantity. What is the equilibrium price in this market, and which firm has higher profits?
(a) p = 10, and firm 1 has higher profits
(b) p = 10, and firm 2 has higher profits
(c) p = 32/3, and firm 1 has higher profits
(d) p = 32/3, and firm 2 has higher profits
(e) p = 9, and firm 2 has higher profits
11. Assume that there are two entrepreneurs and that the first one moves first, exactly as above. But now the cost curves are C1 (q1 ) = 4 + 6q1 and C2 (q2 ) = 8 + 4q2 : that is, there are fixed costs. In addition, we’ll allow for explicit entry decisions. If they do not enter, they get a payoff of zero (that is, they avoid paying the fixed cost). Thus, you can think of this as a game with up to four stages: (1) Firm 1’s entry decision; (2) Firm 1’s quantity decision, if it entered; (3) Firm 2’s entry decision, given Firm 1’s choices; (4) Firm 2’s quantity decision, if Firm 2 entered. Assume that, if firm 2 is indifferent between entering the market or not (that is, total profits after entering are zero), then it does NOT enter.
What is the equilibrium price in this market?
(a) p=9
(b) p=10
(c) p=11
(d) p=12
(e) p=13
12. There are two entrepreneurs with identical cost curves C(q) = 10 + 8q. The game has two rounds. In the first round, they simultaneously decide whether to enter or not. A firm that does not enter gets a profit of zero. In the second round, the firm(s) that enter observe whether the other has entered as well or not. Then, they decide quantities (simultaneously, if both enter).
Is there a mixed-strategy Nash equilibrium in this market where firms are indifferent between entering or not, and if so,what is the probability that firms enter?
(a) There is no such mixed strategy Nash equilibrium.
(b) There is an equilibrium, and each firm enters with probability 1/5.
(c) There is an equilibrium, and each firm enters with probability 2/5. (d) There is an equilibrium, and each firm enters with probability 1/3.
(e) There is an equilibrium, and each firm enters with probability 4/5.
13. Now consider an infinitely repeated game between two entrepreneurs with identical cost curves: C(q) = q + 1 if they produce q > 0, or zero otherwise. That is: in every round they operate, they must pay the fixed cost. If they don’t operate in that round, they avoid the fixed cost. They have a common discount factor δ ∈ (0, 1). They are considering a collusive agreement where they take turns operating in the market: firm 1 in ”odd” rounds starting with the first, and firm 2 in ”even” rounds starting with the second. In the rounds where they operate, they choose the monopolist quantity. If a firm deviates from the agreed-upon quantities and timing, they stop alternating and play the static Cournot strategy forever. Consider the following statements (a)-(c) below. If exactly one of them is correct, choose that option. If none of them are correct, choose option (d). If more than one are correct, choose option (e). Hint: solving the math of this problem can take a lot of time-but you can probably solve it without any math.
(a) This strategy profile can be a subgame-perfect Nash equilibrium if δ is high enough.
(b) If δ is close to 1, then this proposed strategy profile achieves higher payoffs for the firms than an alternative collusive strategy where both operate in all rounds, each producing half of the monopolist quantity. That’s because they can cut their expenditures in fixed costs by half if they only operate every other round.
(c) The firm that starts first has a higher total payoff for the game.
(d) None of (a)-(c) are correct.
(e) More than one of (a)-(c) are correct.
Info for items 14 and 15: Assume that firm 1 has cost curve C1 (q1 ) = 4 + q1 . In the first stage of the game, that firm decides whether to enter or not, and how much quantity to produce. If it does not produce anything, it avoids paying the fixed cost. In the second stage of the game, a very large number of other entrepreneurs decide simultaneously whether to produce or not, and if so, how much (after observing the first firm’s quantity). These ”followers” have identical cost curves Cf (qf ) = 2qf . They have no fixed costs, but marginal costs are higher compared to the first one. Note that the followers can decide to produce even if the first firm does not.
14. Does the first firm enter the market (that is, does it choose a quantity larger than zero), and if so, what option best approximates the quantity it chooses?
(a) The first firm does not enter.
(b) The first firm enters and chooses exactly or approximately q1 = 2.8
(c) The first firm enters and chooses exactly or approximately q1 = 4.5
(d) The first firm enters and chooses exactly or approximately q1 = 9
(e) The first firm enters and chooses exactly or approximately q1 = 6.4
15. Suppose that a regulator could prohibit the first firm (with low cost) from entering the market. If it did that, what would happen to consumer surplus and the number of firms in operation?
(a) Consumer surplus would fall, and the number of firms in operation would fall
(b) Consumer surplus would fall, and the number of firms in operation would rise
(c) Consumer surplus would stay the same, and the number of firms in operation would fall
(d) Consumer surplus would stay the same, and the number of firms in operation would rise
(e) Consumer surplus would rise, and the number of firms in operation would rise
Second long question
In the 2000’s, the Brazilian national government implemented an audit program to detect political corruption at the city level. After prominent political economists used econometrics to show that the program was successful, the government is deciding to do it again. To do so, they need to design the program and advertise it, incurring in some fixed costs F. On top of that, for each city that the government decides to inspect, it must pay additional costs c, corresponding to training inspectors, paying for their wages during the inspection, and travel costs.
In each city, the mayor may choose to steal or not. If the mayor steals and there is no inspection, he gets a benefit of B, which corresponds to a loss of the same magnitude from the point of view of the national government. If the mayor steals and there is a inspection in the city, the mayor does not get the benefit B: it is forced to pay back the money to the government. On top of that, the mayor gets a negative payoff −P corresponding to the punishment for corruption. Assume that P > B > c > 0.
16. Consider the payoffs for the mayor and the national government corresponding to corruption in one particular city, in the scenario where the government has re -created the program and may choose to send an inspector to the city. What matrix below represents these payoffs correctly? Note fixed costs should not be factored in.
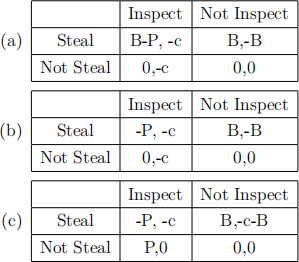
(d) It is not possible to represent the payoffs in a matrix.
(e) None of the options above is correct.
17. Now model this problem as a sequential game, where the players are the national government and a number N of mayors. In the first stage, the government decides to fund the program or not, paying fixed cost F. The mayors observe whether the program is funded or not. In the second period, each of the mayors decides to steal or not. If the government decides to fund the program, in the second stage they may choose to inspect each particular city or not. The inspection and stealing decisions are simultaneous. If the government does not fund the program, then it cannot inspect any city.
Think about the subgame perfect Nash equilibrium of this game, allowing for mixed strategies. Which of the following statements is accurate?
(a) The equilibrium level of corruption decreases with P.
(b) It is irrational for mayors to engage in corruption if the government funds the program.
(c) The government will fund the program only if (B − c)N ≥ F.
(d) It is never optimal for the government to fund the program.
(e) There is no subgame perfect Nash equilibrium for this game.
18. Now consider a modified sequential game. In the first stage, the government decides whether to fund the program. In the second stage, it commits to a probability of au- diting each city. Specifically, the government announces the probability to the public, and years later (when it’s time for the audits), they conduct a public lottery live on TV that determines which cities will be audited. In the third stage, after knowing the probability of auction but before knowing if their particular city will be audited, the mayors decide whether to steal or not. Assume that F is low enough that the government will fund the audits program.
Thinking about the differences between this game and the one from the previous ques- tion, which of the following statements is correct?
(a) There is a subgame perfect Nash equilibrium with zero corruption, and the ex- pected payoff for the government is larger than in the game from the previous question.
(b) There is no subgame perfect Nash equilibrium.
(c) There is a subgame perfect Nash equilibrium in which some mayors engage in corruption.
(d) There is a subgame perfect Nash equilibrium with zero corruption, but the ex- pected payoff for the government is smaller than in the game from the previous question.
(e) Knowing the probabilities with certainty improves the expected outcomes of may- ors, compared to the previous game where the probabilities and stealing where decided simultaneously.