EC9900
May Examinations 2021/22
Topics in Applied Macroeconomics
Section A: Answer the ONE question
1. Answer all parts of the question:
(a) Consider the partial equilibrium search model with exogenous job destruction studied in the lectures. The Bellman equations for a worker are given by:
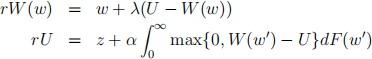
where:
– W(w) is the value of being employed at wage w
– U is the value of being unemployed
– w is the flow wage
– z is the flow utility or income during unemployment
– r is the discount rate
– λ is the job-separation rate
– α is the rate at which an unemployed worker meets a job
– F(.) is the cdf of offered wages
(i) Explain what is meant by a reservation wage in this model. Explain why the worker’s problem is characterized by a unique reservation wage. (4 marks)
As seen in the lecture, the worker’s reservation wage, wR, in this model is the solution to the equation:
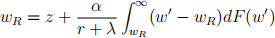
(ii) Consider an increase in the flow utility during unemployment, z. Show analytically how this affects the reservation wage. Explain intuitively. (6 marks)
(iii) Find expressions for the job-finding rate, the average unemployment duration and the steady-state unemployment rate as in terms of the reservation wage, wR, and parameters. Show how an increase in z affects each of these. (6 marks)
Now suppose that the labour force consists of two types of workers who differ only by their flow utility during unemployment, z. There are L H workers with flow utility z H and L L workers with flow utility z L where z H > zL and L H and L L are constant parameters. Hence, the two types of workers have different reservation wages defined implicitly by:
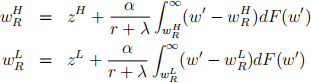
A worker of each type can be employed or unemployed. Let there be E j employed and Unj unemployed workers of type j ∈ {H, L} so L j = E j + Unj , ∀j ∈ {H, L}.
The aggregate unemployment rate in the economy is defined as:
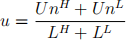
The unemployment rate for workers of type j is defined as:
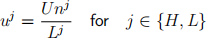
In the steady state of the model both the aggregate unemployment rate and the unemployment rates for each type of worker are constant.
(iv) Find expressions for the steady-state unemployment rates for workers of type H and L in terms of the parameters and the reservation wages. (3 marks)
(v) Find an expression for the steady-state aggregate unemployment rate in terms of the parameters and the reservation wages. Which of the three unemployment rates is highest and which is lowest? (6 marks)
(b) Based on the discussion of Shimer (2012) briefly explain how one can quantify the relative contributions of the fluctuations of job-finding and job-separation rates to fluctuations of the unemployment rate. (8 marks)
(c) Describe the key empirical regularities in the long-run evolution of unemployment rates in OECD economies over the decades prior to the Great Recession. Making reference to specific empirical facts, discuss briefly how Ljungqvist and Sargent (1998) explain key aspects of the observed patterns. (17 marks)
Section B: Answer the ONE question
2. Answer all parts of the question:
(a) Blundell et al (2014) are interested in the determinants of recent changes in productivity. Consider a world with two time periods t = 0 and t = 1. Suppose the authors have data on log wages for individuals indexed by i, wit, and a vector of characteristics Xit. The log wage equation is given by:
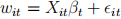
(i) Using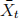 
and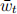 
to denote the average characteristics and log wage across individuals at time t, write out a Oaxaca-Blinder decomposition for the difference in log wages between the two time periods, 
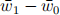. Explain the different parts of your decomposition in the given setting. (6 marks)
(ii) Is your decomposition from part (i) unique? Write out an alternative way of decomposing log wages, explaining the different parts of your decomposition. (3 marks)
(b) Suppose there are two types of workers, low skilled and high skilled, in an economy. The production function for the aggregate economy has a constant elasticity of substitution (CES) form:
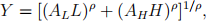
where Y is aggregate output, L denotes the supply of low skilled labour, H denotes the supply of high skilled labour. AL and AH denote the productivity of low skilled and high skilled labour, respectively, and ρ ≤ 1 is a parameter of the production function.
Define σ as the elasticity of substitution between the two types of labour: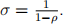 
.
Assume that labour markets are perfectly competitive.
(i) Derive the wages for low skilled and high skilled labour, wL and wH. (4 marks)
(ii) Using your answer from part (i), derive the skill premium of high skilled over low skilled labour. Write out the log skill premium. What happens to the log skill premium when the log supply of high skilled to low skilled workers increases? Provide an intuition. (6 marks)
(iii) What happens to the CES production function as ρ → 1? What happens to relative wages? Provide an intuition. (5 marks)
(iv) Explain what is meant by ”labour market polarisation”. Discuss the causes of this phenomenon. (8 marks)
(c) Consider the Mariel Boatlift discussed in lectures. Explain what happened in Miami in 1980 and why the event was considered a natural experiment to analyse the effects of immigration. Discuss the evidence around this event provided by Card (1990). What did he find? How can the results be explained? Discuss the more recent evidence on the effects of the Mariel Boatlift. (18 marks)