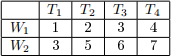Hello, if you have any need, please feel free to consult us, this is my wechat: wx91due
MATH367 Specimen Class test I
Problem 1: Tree graphs and planar graphs
1. Describe tree graphs that correspond to the Prüfer sequence P = (2, 3, 4,..., n−2, n−1), with n some positive integer number. (3 points)
2. Prove that any tree graph is a planar graph (2 points) .
3. Prove that we obtain a planar graph by adding one more edge to any tree graph (without changing the number of vertices) (2 points) .
Problem 2: Eulerian and Hamiltonian graphs
1. Construct an Eulerian trail for the following graph: (4 points)
2. Which tree graphs are Hamiltonian graphs? (2 points)
Problem 3: Minimal spanning trees and shortest-distance paths
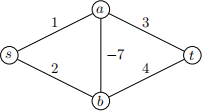
Consider the following network N :
N consists of four vertices {s,a,b,t} and ve edges {{s,a} , {s,b} , {a,t} , {b,t} , {a,b}} with the weights wt({s,a}) = 1, wt({s,b}) = 2, wt({a,t}) = 3, wt({b,t}) = 4, wt({a,b}) = −7.
1. List all cycles of N and their weights. (2 points)
2. Apply the Prim's (2 points) and the Kruskal's (2 points) algorithms to nd the minimal spanning tree of N. Apply Dijkstra's algorithm to nd the shortest path between the vertices s and t (2 points) . If some of these algorithms are not applicable to the network N , explain why.
Problem 4: Assignment problem
Two workers W1 and W2 are capable of performing n1 = 1 and n2 = 2 tasks, respectively. They need to accomplish as many tasks as possible out of the four tasks T1 , T2 , T3 and T4 . Each task can be accomplished by one worker only. The cost of performing the task Tj by the worker Wi is given in the table below:
Use a cost ow network to nd out how to accomplish the maximal pos- sible number of tasks at the least possible cost. (7 points) Discuss whether your assignment is unique and justify your answer. (2 points)