MATH. 117
Practice Problems 1
Jan. 2024
The midterm will not have this many questions!
1. Give a complete and accurate definition (not just notation) for the term below. (Do not give the conditions from some theorem either, only the basic definition, as stated when the term was first introduced.)
A sequence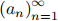 
converges to a number A iff :
2. Carefully and accurately state (but do not prove) the indicated item. Be sure to put in all the hypotheses, and the complete conclusions.
The lemma expressing convergence in terms of neighborhoods.
3. No proofs required for this question.
(a) Give an example of an infinite set with no accumulation points.
(b) Give an example of divergent sequences
and
such that
is convergent.
(c) Carefully describe what it means that a number A is not an accumulation point of a set S.
4. Using only the definition of convergence, prove the following theorem which we estab-lished in class:
If a sequence 
converges to A and also converges to B, then A = B.
5. Prove that the sequence 
diverges.
6. Let A ∈ R, and suppose Q is a neighborhood of 2A − 3. Show that the following set U = {x ∈ R | 2x − 3 ∈ Q} is a neighborhood of A.
7. Suppose that S and T are nonempty subsets of R which are bounded below, and that S ⊆ T. Prove that inf S ≥ inf T.
8. Let S ⊆ R be a nonempty set which is bounded below, and let y = inf S. Show that for every ε > 0, there exists a ∈ S such that y ≤ a < y + ε.
9. Give a direct proof, using only the definition of “Cauchy sequence”, of the following statement. Do not use theorems about convergence.
If
and
are Cauchy sequences, then
is Cauchy.
10. Using only the definition of convergence, prove the following theorem which we estab-lished in class:
If