ECON33001
MACROECONOMICS OF DEVELOPMENT
Semester One, 2023
1. Consider the following production function for human capital
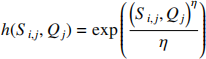
where Si,j is the years of schooling of worker i in country j, Qj is quality of schooling in country j, 0 < η < 1 is an elasticity parameter.
To carry out development accounting we need an estimate of human capital. We have sample of migrants from a number of countries working in the US. We also have sample of workers for the same countries working in their home country. The samples of workers working in the US and working at home consist of different workers. The information about each worker in the samples include wages, years of schooling and a set of wage relevant characteristics.
However, we do not observe school quality in country j, Qj,and the elasticity η,which is common across countries.
2. Consider a two–sector version of the growth model with agricultural and manufactured goods. Time is discrete and runs forever and there is a continuum of measure one of identical households. The utility function is given by(a) [12 MARKS] To construct human capital we need to estimate the returns to years schooling. Explain why it is crucial for estimating the returns to schooling to assume that different types of human capital are perfect substitutes in the production process.
(b) [12 MARKS] How do we estimate on the data the returns to years of schooling?
(c) [12 MARKS] Suppose we estimate the return to years of schooling on all of our sam-ples. How μj can be linked to the above production function for human capital, and to the quality of schooling Qj?
(d) [14 MARKS] How would you estimate η and ultimately construct human capital. Hint: We have two samples for each country. The sample of migrants in the USA and the sample of non-migrants. We estimated for return to schooling, μj(US) and μj.
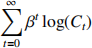
where the consumption aggregator is

and µ and C¯ are positive constants. The production functions for agricultural and manufac-tured goods take the form
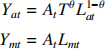
where T = 1 island, Lat + Lmt = 1 is total labor, and At is total factor productivity. At grows at a constant factor γ > 1.
(a) [12 MARKS] Argue that A0 > C¯ is a necessary condition for an interior equilibrium, thus, an equilibrium with positive employment in both sectors.
(b) [12 MARKS] Derive the equilibrium conditions, and show that along the equilibrium path, laboris reallocated from agriculture to manufacturing (“structural transforma-tion”). Provide intuition for why structural transformation takes place in this econ-omy.
(c) [12 MARKS] Show that the growth rate of real GDP, Yt = Pt Cat + Cmt , is decreasing over time. Provide the intuition for why that is the case.
(d) [14 MARKS] Land owners are often opposed to structural transformation. Suggest how to modify this model so that it can be used to provide an explanation for their opposition.