Hello, if you have any need, please feel free to consult us, this is my wechat: wx91due
ECS122A Problem Set #6
Due: 11:59pm, June 3, 2024
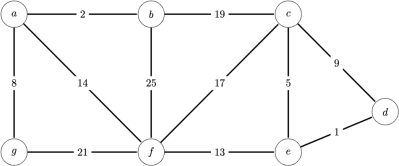
1. Run Prim’s algorithm with the root vertex a for finding the minimum spanning tree on the following graph; whenever there a choice of nodes, always use alphabetic ordering. Mark on the graph showing the intermediate values, and list the final minimum spanning tree.
2. Prove or disprove: Prim’s MST algorithm will work correctly even if weights maybe negative.
3. Run Kruskal’s algorithm for finding the minimum spanning tree on the graph shown in Prob- lem 1. List the order of edges adding to the MST, i.e., the set A.
4. Show how to find the maximum spanning tree of a undirected connected weighted graph G = (V, E), that is, the spanning tree of largest total weight.
5. (a) Run the Bellman-Ford algorithm on the following directed graph, using vertex y as the source. Relax edges in lexicographic order in each pass. Draw a table showing the d and π values after each pass.
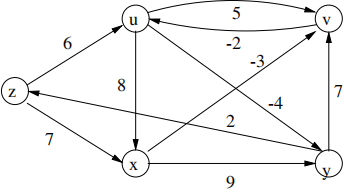
(b) Change the weight of edge (y, v) to 4 and run the algorithm again, using z as the source.
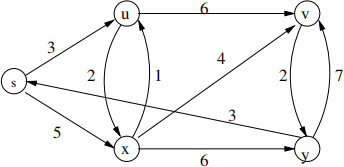
6. Run Dijkstra’s algorithm on the following directed graph,
(a) first using vertex s as the source, and (b) then using vertex y as the source.
Mark on the graph showing the intermediate values, and list the final shortest-path.
7. Give a simple example of a directed graph with negative-weight edges for which Dijkstra’s algorithm produces incorrect answers.
8. We are given a directed graph G = (V, E) on which each edge (u, v) ∈ E has an associated value r(u, v), which is a real number in the range 0 ≤ r(u, v) ≤ 1 that represents the reli-ability of a communication channel from vertex u to vertex v. We interpret r(u, v) as the probability that the channel from u to v will not fail, and we assume that these probabilities are independent. Given an efficient algorithm to find the most reliable path between two given vertices.
9. The bin packing decision problem is that given an unlimited number of bins, each of capacity 1, and nobjects with sizes s1 , s2 , . . . , sn, where 0 < si ≤ 1, do the objects fitin k bins? where k is a given integer.
The bin packing optimization problem is to find the smallest number of bins into which the objects can be packed.
Show that if the decision problem can be solved in polynomial time, then the optimization problem can also be solved in polynomial time.
10. Show that if the hamiltonian cycle decision problem can be solved, then the problem of listing the vertices of a hamiltonian cycle in order is also solvable.
11. Suppose that we had a polynomial-time subprogram TSP to solve the traveling saleperson decision problem (i.e., given a complete weighted graph and an integer k, it determines whether there is a tour of total weight at most k.)
(a) Show how to use the TSP subprogram to determine the weight of an optimal tour in polynomial time.
(b) Show how to use the TSP subprogram to find an optimal tour in polynomial time.
12. (Optional) A graph G = (V, E) is said to be k-colorable if there is a way to paint its vertices using k diferent colors such that no adjacent vertices are painted the same color. When k is a number, by k-COLOR we denote the decision problem of k-colorable graphs.
(a) Give an efficient algorithm to determine a 2-coloring of a graph if one exists.
(b) The 3-COLOR problem is known to be NP-complete. Use this to prove that the 4-COLOR is NP-complete.