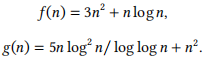COSC 320 Assignment 1 Problems
Covering introduction and asymptotic notation.
January 12, 2024
This assignment is due on Friday, Jan 26 at 10pm Kelowna time on Canvas. Assignments submitted after this deadline, will receive a penalty or won’t be accepted. Please see course outline for details. Please follow these guidelines:
• We strongly recommend that you prepare your solution using LATEX, and submit a pdf file. We will accept solutions that are prepared using other good formatting systems, as long as they are clearly legible. Solutions that are handwritten or difficult to read will receive a grade of zero.
• Whenever possible, keep the solution to a subproblem on a single page, rather than having it span two pages.
• Include in question 1 below the names of each member of your team. You need to form teams, which will be recorded on Canvas. If you want an extra double-check on your identity, include your student number. Reminder: groups should include a maximum of three students; we encourage groups of two.
• Start each problem on a new page, using the same numbering and ordering as this handout.
• Submit the assignment via Canvas. Your group must make a single submission.
• If you include the problem definitions, we would also appreciate it if you could typeset your solutions in blue, as it makes it easier for TAs to find the solutions.
Before we begin, a few notes on pseudocode. Your pseudocode should communicate your algorithm clearly, concisely, correctly, and without irrelevant detail. Reasonable use of plain English is fine. You should envision your audience as a capable COSC 320 student unfamiliar with the problem you aresolving. Don’t include what we consider to be irrelevant detail.
Remember also to justify/explain your answers, unless explicitly indicated otherwise. We understand that gauging how much justification to provide can be tricky. Inevitably, judgment is applied by both student and grader as to how much is enough, or too much, and it’s frustrating for all concerned when judgments don’t align. Justifications/explanations need not belong or formal, but should be clear and specific (referring back to lines of pseudocode, for example). In this class the words “prove”, “explain”, “show” and “justify” are used interchangeably; we’re not looking for the formality that might be expected in a Math class. You don’tneed to be more formal when a proof is requested, but sometimes formal notation or assertions can really help make concepts clear and unambiguous.
On the plus side, if you choose an incorrect answer when selecting an option but your reasoning shows partial understanding, you might get more marks than if no justification is provided. And the effort you expend in writing down the justification will hopefully help you gain deeper understanding and may well help you converge to the rightselection :)
Ok, time to get started...
1 List of names of group members (as listed on Canvas)
Provide the list here. This is worth 1 mark. Include student numbers as a secondary failsafe if you wish.
2 Statement on collaboration and use of resources
To develop good practices in doing homeworks, citing resources and acknowledging input from others, please complete the following. Answer Yes or No to each question below. This question is worth 2 marks.
1. We used the following resources (list books, online sources, etc. that you consulted):
2. One or more of us consulted with course staff during office hours.
3. One or more of us collaborated with other COSC 320 students; none of us took written notes during our consultations.
If yes, please list their name(s) here:
4. One or more of us collaborated with or consulted others outside of COSC 320; none of us took written notes during our consultations.
If yes, please list their name(s) here:
3 Big-O Analysis: Algorithms on Numbers
Let x and λ be two nonnegative integers, represented in binary. Assume for concreteness that there are no leading zero’s in the binary representations; for example the number three is represented as 11 and not as 00011. (If you prefer, you can assume that the numbers are represented in decimal and answer the problem for decimal addition and division operations, it won’t change the answer.)
1. Addition. A standard algorithm for adding x and λ produces the sum x + λ by working from low-order bits to high-order bits of each number. A carry bit is initially set to 0. The algorithm iteratively produces an output bit from the carry and two bits of x and λ (or just one of these if all bits of the other have already been considered),and updates the carry. Once all bits of x and λ are considered, if the carry is 1, then a final high-order 1 is output.
(a) (2 marks) Give a tight big-
bound on the running time of this algorithm as a function of x and λ. Justify your answer. You may assume that you can access the bits of the numbers in constant time (i.e., you can get the value of the!th bit for any !).
(b) (2 marks) Which categories does the running time of the standard addition algorithm belong to? Choose as many as apply. (Your justification for your choices need not consider all options separately; may be able to justify your choices across a row with one sentence, using facts that you already know about the growth of functions.)
O(xy) O(x + y) O(IogxIog y) O(Iogx + Iog y)
o(xy) o(x + y) o(IogxIog y) o(Iogx + Iog y)
2. Least Common Multiple. Algorithm LCM finds the least common multiple of x and λ:
procedure LCM(x, λ)
m ← max{x, λ}
while (m moqx ≠ 0) or (m moq y ≠ 0) do
m ← m + I
end while
return m
end procedure
(a) (2 marks) Give a tight big-o bound on the number of times that the mod operation is applied in the LCM algorithm, as a function of x and λ. Justify your answer.
(b) (2 marks) Describe an infinite set of pairs (x, λ) for which the number of times that the mod operation is applied iso(I).
(c) (2 marks) Which of the following categories describe how many times the mod operation is executed? Choose as many as apply, and justify your answer.
O(xy) O(x + y) O(IogxIog y) O(Iogx + Iog y)
Θ(xy) Θ(x + y) Θ(IogxIog y) Θ(Iogx + Iog y)
4 Big O and Big Omega
1. Consider this pair of functions:
Answer the following questions, and provide a justification for your answer in each case.
(a) (2 marks) Is f = Ω(g)?
(b) (2 marks) Is g = Ω(f)?
2. (2 marks) Do there exist functions f, g, and ℎ such that f is not big-O of g, g is not big-O of ℎ, but f is big-O of ℎ? Justify your answer.