Faculty of Business and Economics
FINA2312—Advanced Corporate Finance
Assignment 2
Due: March 5, 2024
1. Consider a firm whose stock price at the end of the year depends on the state of the economy (good or bad with equal probability) and the outcome of a lawsuit (win with probability 0.8 and lost with probability 0.2):
The firm’s current stock price (i.e., at the beginning of the year) is $2 per share. The riskless rate of interest is 10% per year.
(a) Form a tracking portfolio using the underlying stock and the riskless asset to evaluate a European call option on this stock, which expires at the end of the year with the strike price set equal to $3.5.
(b) Show that there are tracking errors in part (a). Why don’t you worry about the tracking errors?
2. Consider a stock which is currently selling at $4.5. The stock price will either go up to $5 + x with probability 0.5 or go down to $5 − x with probability 0.5 one period later. The one-period riskless rate of interest is 5%.
(a) What are the market prices of at-the-money call options that expire at the end of the period when x is set equal to $0.5, $1, $1.5, $2, and $2.5, respectively?
(b) Plot the one-period call option prices against the five possible values of x.
(c) What is the reason for the pattern that you find in part (b)?
(d) Redo parts (a) to (c) for at-the-money put options that expire at the end of the period.
3. Suppose that you own a piece of property in New Territories, and similar parcels of land near yours have sold recently for $10 million. A developer has approached you and asked you for a one-year option to purchase the property at the prespecified price of $12.5 million. The required rate of return on land, µ, is 10% per year and the standard deviation of log returns on land, σ, is 25% per year. The expected log return on land, m, is 6.875% per year. The riskless rate of interest, r, is 5% per year. All compounding and discounting are done in continuous time.
(a) Build a 6-step binomial tree by using the multiplier for an up step equal to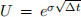 
and that for a down step equal to 
, where ∆t is the length of time for each binomial time step.
(b) Use the formula that the subjective probability of an up step is equal to
Compute the expected value of the land after one year based on the binomial tree in part (a) under the subjective probability distribution.
(c) What are the expected rate of return on the land per year and the expected log return on the land per year implied by your answer in part (b)?
(d) Use the formula that the risk-neutral probability of an up step is equal to
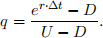
Compute the expected value of the land after one year based on the binomial tree in part (a) under the risk-neutral probability distribution.
(e) What are the expected rate of return on the land per year and the expected log return on the land per year implied by your answer in part (d)?
(f) What is the present value of the one-year option to purchase the property at the strike price of $12.5 million based on the binomial tree in part (a)?