Hello, if you have any need, please feel free to consult us, this is my wechat: wx91due
EC333 Topics in Financial Economics: Theories and International Finance
PROBLEM SET 3
CAPM
1) Suppose that in the economy there are three securities: (i) two stocks Intel and Microsoft and (ii) a risk free asset. The risk free rate is 5%. The information about return and the variance covariance for Intel and Microsoft is given by the following:
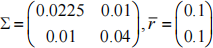
Note- In the above we assume that the first security is Intel so for example the variance of Intel is 0.0225.
a) What is the tangency portfolio and what is the highest Sharpe ratio that one can obtain? You can either use Excel spreadsheet or use the formula provided below.
b) Suppose that Microsoft and Intel are the only stocks in the economy and the Market cap of both firms is $100B. Is the above information consistent with CAPM? Explain.
c) In contrast to b) suppose that there are many stocks in the economy and the data
above is still the data for Intel and Microsoft. How would your answer to b) change?
Note: The formula for inverting a 2x2 non-diagonal matrix is given by
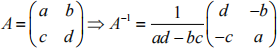
2) Implications of CAPM
The riskless rate of interest is .06 per year, and the expected rate of return on the market portfolio is .15 per year.
a) According to the CAPM, what is the efficient way for an investor to achieve an expected rate of return of .10 per year?
b) If the standard deviation of the rate of return on the market portfolio is .20, what is the standard deviation n the foregoing portfolio?
c) Draw the CML and locate the foregoing portfolio on the same graph. d) Draw the SML and locate the foregoing portfolio on the same graph.
e) Estimate the value of a stock with an expected dividend per share of $5 this coming year, an expected dividend growth rate of 4% per year forever, and a beta of 0.8. If its market price is less than the value you have estimated (i.e., if it is underpriced), what is true of its mean rate of return?
3) If the CAPM is valid, which of the following situations is possible? Explain. Consider each situation independently.
a) Portfolio Expected Return Beta
A .20 1.4
B .25 1.2
b) Portfolio Expected Return Standard Deviation
A .30 .35
B .40 .25
c) Portfolio Expected Return Standard Deviation
Risk free .10 0
Market .18 .24
A .16 .12
d) Portfolio Expected Return Standard Deviation
Risk free .10 0
Market .18 .24
A .20 .22