ECON 3208 Game Theory

QUESTION 1

Consider the following simultaneous game.

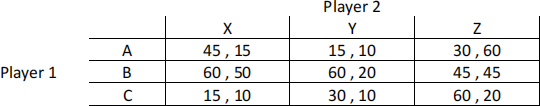
a.    [2 pts] For each player, indicate if any strategies are strictly dominant. Briefly explain your answer.

b.    [2 pts] For each player, indicate if any strategies are strictly dominated. Briefly explain your answer.

c.    [3 pts] For each player, indicate if any strategies are weakly dominant. Briefly explain your answer.

d.    [7 pts] List all pure-strategy Nash equilibria of the above game.

e.    [3 pts] Does your answer to part (d) change if Player 1’s payoff of playing B doubles? Briefly explain your answer.

f.     [3 pts] Is the following statement true or false (explain your answer):  In any strategic-form game, if a player has a dominant strategy, then all of the other strategies of that player are dominated.

QUESTION 2

Two candidates are at a debate. They could either sabotage each other or make policy suggestions (stay on the higher ground). Depending on what they choose, their approval rates will change in the following manner:

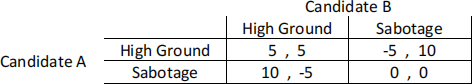
a.    [4 pts] What makes a game prisoner’s dilemma? Is this game a prisoner’s dilemma? Explain.

b.    [3 pts] Imagine that the two candidates play this game for a finite number of years. When will they choose to have a debate over policies? Explain.

Suppose the two candidates play this game annually and forever using the grim trigger strategy.

c.    [8 pts] For what range of patience levels would we expect cooperation? Show your work.

d.    [2 pts] For what range of interest rates would we expect cooperation? Show your work.

e.    [3 pts] If the two countries use the tit-for-tat strategy instead, is the range of interest rates that induces cooperation smaller than your answer to part (d)? Explain.

QUESTION 3

Consider the following game.

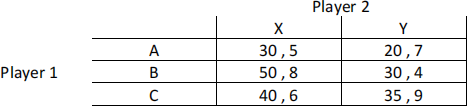
a.    [8 pts] Imagine that Player 1 makes a decision first and Player 2 makes a decision after observing Player 1’s choice. Write down the sub-game perfect Nash equilibrium of this game.

b.    [7 pts] Is there a first-mover advantage in this game? Carefully explain.

c.    [5 pts] Is there a second-mover advantage in this game? Carefully explain.

QUESTION 4

Consider the stag hunt game we covered in class.

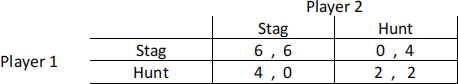
a.    [3 pts] How many Nash equilibriums do we have in this game?

b.    [7 pts] In the game above, what is Player 2’s Mixed Strategy Nash equilibrium strategy? Demonstrate or explain.

c.    [4 pts] In the game above, what is Player 1’s Mixed Strategy Nash equilibrium expected payoff? Show your work.

Suppose Player 1 becomes opportunistic too, which increases his payoffs for the top-right corner and the bottom-left corner.

d.    [6 pts] Explain if and how this would change Player 1’s Nash equilibrium strategy in this game. [Numeric answers are okay but not necessary.]