Hello, if you have any need, please feel free to consult us, this is my wechat: wx91due
COMP9123 Assignment 4
S1 2024
This assignment is due on May 10 and is only for COMP9123 (postgraduate) students. This assignment should be submitted via Gradescope. All submitted work must be done individually without consulting someone else’s solutions in accordance with the University’s “Academic Dishonesty and Plagiarism” policies.
The main purpose of this assignment is to see your programming skills (pseu- docode). While you can do this assignment just writing in English (with full marks), it is encouraged to use pseudocodes (and comments). Do not forget to read the sec- tion: “Advice on how to do the assignment.” As an aside, if you need a general refresher or have some specific questions, please ask on Ed.
Question 1 [20 pts]
Given an undirected graph G = (V, E) with n vertices and m edges, and a positive (not necessarily unique) edge cost ce for each edge in E. We are also given q pairs of vertices Q = {(u1, v1), . . . , (uq, vq )}. Decide for each pair (u, v) in Q if there is a path between u and v in G.
Implement your algorithm using the following format:
n
m
vertexId vertexId weight (between those two vertices)
vertexId vertexId weight (between those two vertices)
...
vertexId vertexId weight (between those two vertices)
q
vertexId vertexId (the vertices you want to find if they are linked or not) vertexId vertexId (the vertices you want to find if they are linked or not)
...
For example, the text below describes the instance depicted in Fig. 1. Note that the vertices are numbered from 0 to n − 1 and that the two queries are (0, 1) and (0, 2).
4
3
0 2 2
0 3 5
2 3 3
2
0 1
0 2
Your algorithm should read the input and only needs to print out ‘ 1’ (= yes, there is a pathin G between u and v) or ‘0’ (= no, there is no path connecting u and v in G) for each of the q query pairs. You should separate each 1/0 with a new line. Additionally, if there is a path that connects the two vertices you should include the total weight of the path you took.
If the query is (0, 1) on the figure 1 below then the answer should be ‘0’ while the answer to the query (0, 2) on the same graph should be ‘1,2’ (one because there is a path, and two because it is the sum of the weights of the path from 0 to 2).
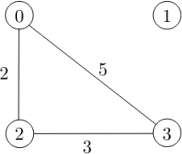
Figure 1: Illustrating the graph described in Question 1, with n = 4 and m = 3.
a) Design an algorithm that solves this problem in O(q · (m + n)) time. (8 points) b) Briefly argue the correctness of your algorithm. (8 points)
c) Analyse the running time of your operations. (4 points)
Question 2 [40 pts]
Consider the following variant of the Minimum Spanning Tree (MST) problem. We are given an undirected graph G = (V, E) with n vertices (numbered from 0 to n — 1) and m edges, a positive (not necessarily unique) edge cost ce for each edge in E, and a subset of edges A ⊂ E (note that A may contain cycles). Suppose that E represents a set of possible direct fibre links between vertices and A represents the existing set of direct fibre links between vertices. We would like to find the cheapest way to connect all the vertices into one connected network.
The abstract problem we are interested in solving is to find a subset X ⊆ E / A of edges of minimum cost such that (V, X n A) is connected.
Implement your algorithm using a similar input like question 1, with the follow- ing format (where a is the number of edges in A):
n
m
vertexId vertexId weight
vertexId vertexId weight
...
a
vertexId vertexId
vertexId vertexId
...
For example, the following text describes the instance depicted in Fig. 2. Note that the vertices are numbered from 0 to n − 1.
4
5
0 2 2
0 1 6
0 3 5
1 3 8
2 3 3
2
0 2
1 3
Your algorithm should read the input, and calculate the cost of the solution generated by your algorithm, that is, the cost of the edges in X n A. Your algorithm does not need to return the actual edges, just print out the total cost rounded to two decimal places to standard output.
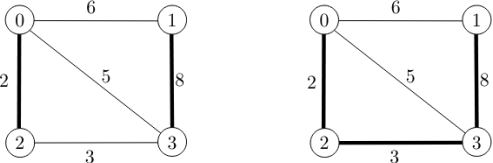
Figure 2: Illustrating the graph described in Question 2, with n = 4, m = 5 and a = 2. Showing an optimal solution having cost 13.
a) Design an algorithm that solves this problem in O(mlogn) time. (16 points)
b) Briefly argue the correctness of your algorithm. (16 points)
c) Analyse the running time of your operations. (8 points)
Advice on how to do the assignment
• Assignments should be typed and submitted as pdf (no handwriting).
• Start by typing your student ID at the top of the first page of your submission. Do not type your name.
• Submit only your answers to the questions. Do not copy the questions.
• When designing an algorithm or data structure, it might help you (and us) if you briefly describe your general idea, and after that you might want to develop and elaborate on details. If we don’t see/understand your general idea, we cannot give you points for it.
• Be careful with giving multiple or alternative answers. If you give multiple answers, then we will give you marks only for "your worst answer", as this indicateshow well you understood the question.
• Some of the questions are very easy (with the help of the lecture notes or book). You can use the material presented in the lecture or book without prov- ing it. You do not need to write more than necessary (see comment above), but you need to reference it or write a couple of lines, it is not enough to men- tion I am using the data structures properties, you need to mention which properties.
• When giving answers to questions, always prove/explain/motivate your an- swers.
• When giving an algorithm as an answer, the algorithm does not have to be given as (pseudo-)code.
• If you do give (pseudo-)code, then you still have to explain your code and your ideas in plain English.
• Unless otherwise stated, we always ask about worst-case analysis, worst case running times etc.
• As done in the lecture, and as it is typical for an algorithms course, we are interested in the most efficient algorithms and data structures.
• If you use further resources (books, scientific papers, the internet,...) to for- mulate your answers, then add references to your sources.
• If you refer to a result in a scientific paper or on the web you need to explain the results to show that you understand the results, and how it was proven.