CS1010S: Programming Methodology
Semester II, 2023/2024
Mission 4
Advanced Recursion
Release date: 16th February 2024
Due: 22nd February 2024, 23:59
Required Files
• mission04-template.py
Background
After demonstrating your abilities to Pharaoh Tyro, you were honored with the presti-gious role of bishop within his esteemed team. The anticipation was palpable as you entered his chambers, where Tyro’s eyes sparkled with expectation. With a grand ges-ture, he handed you three scrolls (Your mission tasks), each bearing the royal seal.
"These," he declared, his voice resonating with authority, "are your inaugural assign-ments as bishop. Execute them diligently and report to me during the upcoming CS1010S class."
This mission consists of three tasks.
Task 1: Number of ways to sum to an Integer (3 marks)
A positive integer n ≥ 2 can be expressed as the sum of a number of positive integers smaller than n. For example:
2 = 1 + 1
3 = 1 + 2
= 1 + 1 + 1
4 = 1 + 3
= 2 + 2
= 1 + 1 + 2
= 1 + 1 + 1 + 1
5 = 1 + 4
= 1 + 1 + 3
= 2 + 3
= 1 + 2 + 2
= 1 + 1 + 1 + 2
= 1 + 1 + 1 + 1 + 1
The function num_sum returns the number of ways that an integer can be expressed as the sum of a number of positive integers. From the above examples, it should be clear that:
>>> num_sum ( 2 )
1
>>> num_sum ( 3 )
2
>>> num_sum ( 4 )
4
>>> num_sum ( 5 )
6
Hint: If you grasp the essence of the count change problem, you’ll recognize that this problem is a variation of it. You may want to consider implementing a helper function that model the count change process of this problem. Solving the problem using closed-form formulas are not allowed.
Task 2: Generalized Pathfinding: Enumerate All Paths (3 marks)
In Lecture Training 5, you faced a problem where you were required to assist Jon in im-plementing a function, num_of_possible_path(board). This function determined the num-ber of possible paths to move from the starting point "S" to the ending point "E" by either walking (covering 1 step) or jumping (covering 2 steps).
Now, you encountered a similar challenge. The game no longer restricts the steps to just 1 or 2; instead, it can be any arbitrary number of steps (i.e. 1, 2, 3, ..., n). Your task is to implement an iterative recursive function, num_of_possible_path(board), which calculates the number of possible paths to move from the starting point "S" to the ending point "E" given that there are n possible ways to move at each step.
You may assume substring(string, start, end, step) function is given.
Hint: Observe that this problem resembles a count change problem. At each step, you have the choice to move 1 step forward, or 2 steps forward, or 3 steps forward, and so on, up to n steps forward.
>>> num_of_possible_path ("S##E", 1 )
1
>>> num_of_possible_path ("S##E", 2 )
3
>>> num_of_possible_path ("S##E", 3 )
4
Task 3: Check valid brackets (5 marks)
Consider a string containing only brackets "(" and ")". A string of brackets is considered valid if:
• Every opening parenthesis has a corresponding closing parenthesis.
• Opening and closing parentheses are in the correct order.
• Each closing parenthesis has a matching opening parenthesis.
Implement a function, check_valid_brackets(s), that returns True if the string s is valid brackets, and False otherwise.
Hint: If a string of brackets is valid, it can repeatedly remove the innermost non-nested "()" until it becomes an empty string.
Subtask 3a: Illustrate Your Problem-Solving Approach
In Lecture 1, you have learnt the Polya’s Problem Solving Process:
1. Understand the Problem
2. Make a Plan (Create a Flowchart, as outlined in Lecture 1 slides)
3. Do the Plan
4. Review & Generalize
Apply the Polya problem-solving methodology, and demonstrate your problem-solving process for Task 3. You are tasked to write out each step, providing insights into your approach and decision-making. This exercise aims to reinforce your understanding and application of the problem-solving methodology.
Please submit your illustration to coursemology. Note that you must include Step 1 and Step 2 in your illustration; Step 3 and Step 4 are optional. (For an example, please refer to Coursemology -> Workbin -> PolyasProblemSolvingExample.pdf)
By using the idea of divide and conquer, here are the steps to solve Task 2
1. Implement an iterative function remove_bracket_pair(s) that takes in a string of brackets. This function iterates through the string from left to right, removing the first occurrence of the brackets pair "()" within the string s, and returns the modified string. You may assume substring(string, start, end, step) function is given.
>>> remove_bracket_pair (" ()()() ")
" ()() "
>>> remove_bracket_pair (" (()()) ")
" (()) "
>>> remove_bracket_pair (" ((())) ")
" (()) "
>>> remove_bracket_pair (")()")
")"
>>> remove_bracket_pair ("()")
""
>>> remove_bracket_pair (" (())((())) ")
" ()((())) "
2. Using the above iterative remove_bracket_pair(s) function, implement a recursive check_valid_brackets(s) that takes in a string of brackets and returns True if the string s is valid brackets, and False otherwise.
>>> check_valid_brackets ("()")
True
>>> check_valid_brackets (" (()) ")
True
>>> check_valid_brackets (" ()() ")
True
>>> check_valid_brackets (" (()")
False
>>> check_valid_brackets (" ())")
False
>>> check_valid_brackets (" ())( ")
False
Subtask 3b: Execute Your Plan
1. Implement the iterative function remove_bracket_pair(s).
2. Implement the recursive function check_valid_brackets(s).
You may assume substring(string, start, end, step) function is given.
You are highly encouraged to test your functions with additional test cases.
Optional: Spiral Maze Iterative Recursively
Write an iterative recursive function num_of_steps that takes in 4 arguments, the x and y coordinates of ending point, x and y, width of the maze, W and height of the maze, H. The function returns the number of steps to navigate from the bottom-left corner (origin) of the maze to the specified ending point. Please follow the question requirements any closed form formula or pure iterative solution will not be accepted.
Hint: You will need to iterate until the boundary, then recursively call the function with the new boundary and updated x & y.
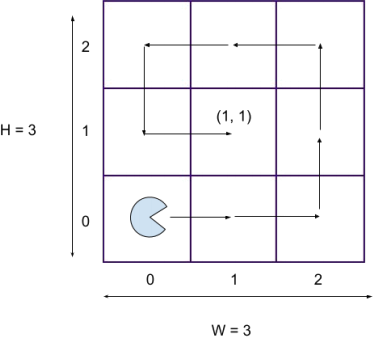
Figure 1: A spiral maze with height 3 and width 3. The number of steps from the origin to the ending point (1, 1) is 8.
num_of_steps (1 , 1 , 3 , 3 )
>>> 8
num_of_steps (0 , 0 , 3 , 3 )
>>> 0
num_of_steps (1 , 1 , 3 , 2 )
>>> 4
num_of_steps (1 , 3 , 5 , 7 )
>>>
Optional: Alternative approach of Task 2
There are many ways to solve the problem in Task 2. You are encouraged to explore alternative approaches to solve the problem.
You may assume substring(string, start, end, step) function is given in this task.
Implement a function, check_valid_brackets_alt(s), that returns True if the string s is valid brackets, and False otherwise.
Completely Iterative Approach (Easy)
You can implement the function purely iterative. Please confine your implementation to what you’ve learned from CS1010S thus far.
Completely Recursive Approach (Challenging)
You may also implement the function purely recursively.
Warning: This is a challenging task.