MATH40082 (Computational Finance)
Main Assignment: Simulation Methods
1 Background
1.1 Stock Options
The trader has calibrated a specialised risk neutral process for some underlying stock price. Given the current stock is S0, market prices indicate the risk-neutral distribution of the stock price at time T is given by:
for some calibrated functions f and v2.
Consider a financial contract C(S, t) written on the underlying asset S with payo↵ on expiry
C(S, T) = g(S).
Then for any given payo↵, the analytic solution may be found by carrying out the numerical integration
To carry out a Monte Carlo valuation of the financial contract, we may use samples from a standard random normal distribution
to write the equation
Then we can simply average out the discounted payoff over n to get our approximation to the value of the financial contract:
where g(S) is the desired payo↵ of the contract.
1.2 Path Dependent Options
Now assume that the risk neutral stochastic process follows the SDE
dS = f(S, t)dt + v(S, t)dW.
The path dependent options you will be pricing depends on S(tk) which are the share prices at K + 1 equally spaced sampling times t0, t1,..., tk = k∆t, ..., tK with t0 = 0, tK = T and
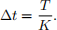
Use an Euler type scheme to write
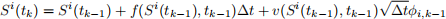
for k = 1, 2, ..., K to estimate the underlying asset values at each time. Here φi,k is a random draw from a Normal distribution.
For path dependent options, the payo↵ function can be written g(S(t0), ..., S(tk), ..., S(tK)) and so the value of the path dependent option can be approximated by
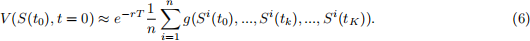
Asian Option
Assume that a discretely sampled Asian option has a payo↵ depending on the discretely sampled average given by
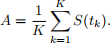
Then we can write
g(S(t0), ..., S(tK)) = G(S(tK), A),
where G(S, A) is the payo↵ function depending the type of option.
There are di↵erent classes of Asian option, resulting in different payoff conditions. In this coursework we look at simple European style call or put options. A fixed strike call option will have the payoff
G(S, A) = max(A − X, 0)
where X is the strike price and a floating strike call option would be
G(S, A) = max(S − A, 0).
where A is sometimes called the average strike price.
A fixed strike put option will have the payo↵
G(S, A) = max(X − A, 0)
where X is the strike price and a floating strike put option would be
G(S, A) = max(A − S, 0).
where A is the strike price.
Lookback Option
The discretely sampled Lookback option has a payo↵ depending on the discretely sampled maximum or minimum given by
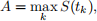
or
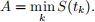
Then we can write
g(S(t0), ..., S(tK)) = G(S(tK), A),
where G(S, A) is the payo↵ function depending the type of option.
There are different classes of Lookback option, resulting in di↵erent payo↵ conditions. In this coursework we look at simple European style call or put options. We can either have a floating strike S or a fixed strike X. For example a floating strike Lookback call option would give
G(S, A) = max(S − A, 0)
where A must be the minimum, and a floating strike Lookback put option would be
G(S, A) = max(A − S, 0).
where A must be the maximum.
A fixed strike call option will have the payo↵
G(S, A) = max(A − X, 0)
where X is the strike price and A must be the maximum. and a fixed strike put option will have the payo↵
G(S, A) = max(X − A, 0)
where X is the strike price and A must be the minimum.
Barrier Options
The discretely sampled knock-out barrier option will be knocked out (and return a value of zero) if the a barrier asset price B is crossed before the maturity date.
The option will be an “up” option if the knock out condition is on S>B, or a “down” option if the condition is on S
Let the variable A be a binary variable such that
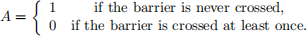
Then we can write
g(S(t0), ..., S(tK)) = A · G(S(tK)),
where G(S) is the payo↵ function depending the type of option.
So for example an up-and-out knockout barrier call option has the payo↵
G(S) = max(S − X, 0)
where
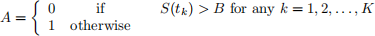
and a down-and-out knockout barrier put option will be
G(S) = max(X − S, 0)
where
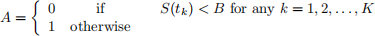
2 Tasks
2.1 Stock Options
You must value a financial contract written on an underlying asset S where the distribution of the stock price at time T is described by the functions
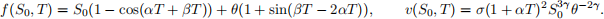
The payo↵ on expiry for the function is
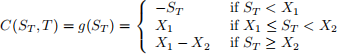
The stock price at time t = 0 is S0 = 95172.9, and the risk-free interest rate is r = 0.04. According to the contract, the option matures at T = 0.5 with strike prices of X1 = 95000 and X2 = 100000. The market fitted parameters are ✓ = 95200, ↵ = 0.06, β = 0.02, γ = 1.04, and the volatility of the option is σ = 0.21.
• Write a program that uses Monte Carlo simulation (5) to approximate the value of the financial contract C and also calculate the value using numerical quadrature (2) both with the parameters stated above. You should state in your report the value of the contract using the analytic solution, and your best estimate for the value of the financial contract using a Monte Carlo approximation. You need only include the code in the appendix of your report. (Coding 3 marks)
• Plot a single figure showing your Monte Carlo approximate of the financial contract value C(S0, t = 0) with increasing n (n = 1000, 2000, ..., 50000, or more!), alongside the exact value from the analytical formula. Comment on the appearance and accuracy of your result. (Understanding 6 marks)
• Write a new program (or programs) that use di↵erent random number generators, antithetic variables, moment matching and/or Halton sequences to approximate the financial contract C and investigate how the accuracy of the approximation changes with di↵erent value of n and how long each calculation takes. You should produce at most 4 plots or tables of your results, and write about them in the text to justify how the methods rank against each other in terms of their efficiency. (Understanding 4 marks, Originality/Initiative 4 marks)
2.2 Path Dependent Options
Now assume that our underlying asset follows the risk neutral process:
where W is a Wiener process and α, β, γ, θ, and σ are all constant parameters determined by the market. Your task is to price a discrete floating-strike Asian put option V with the following parameters. As before, the risk free interest rate is r = 0.04, the market parameters are θ = 95200, α = 0.06, β = 0.02, γ = 1.04 and volatility is σ = 0.21. The stock price is currently S0 = 95172.9, the option matures at T = 0.5 with K = 60 equally spaced observations after the initial time. The floating strike price is the average stock price denoted by A. We do not have an analytic formula to price this option.
• Write a program to approximate the path dependent option V using (6) with the model and parameters as stated above. You should state in the report your best estimate for value of the option using a Monte Carlo approximation. You need only include the code in the appendix of your report. (Coding 2 marks)
• Use your program to generate approximations to the path dependent option V with di↵erent values of n. With the outputs from your calculations you should generate at most 2 plots or tables to investigate the convergence of your result. Comment on your results, state in the text your best estimate of the option value. (Understanding 6 marks)
• Finally, estimate the value of the partial derivative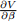 
at S0 and t = 0 using Monte Carlo simulations. You should be able to generate values of V (S0, t = 0; β = 95200) and V (S0, t = 0; β = 95200 + ∆β), so a simple finite di↵erence formula can approximate the derivative:
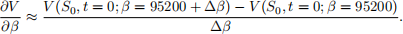
What type of Monte Carlo simulation, what values of N, and what values of ∆β give the most accurate estimate of the value of the derivative? Explain any problems you may find using this formula. State your estimate for the value in the text, you should include up to 2 plots or tables of results to support your result. (Understanding 4 marks, Originality/Initiative 6 marks)
3 Instructions
The deadline for this assignment is 11am on Monday 18th March, and as part of a 15 credit course unit you should expect this may take up to 20 hours to complete. Unless you have an agreed extension on coursework deadlines with DASS reports handed in AFTER 11am Monday 18th March will be docked 4 marks plus an additional 4 marks each day thereafter until a mark of zero is reached. Reports handed in after 5pm Friday 29th March will be awarded a mark of zero and will not be marked.
You must use LATEX to create the document you hand in. Please write your own code and report, you may work together but do not transfer your codes or report files to another student for them to use, via email or by sharing them on cloud hosting websites. To do so would be considered plagiarism and it would carry severe penalties. Please see the university guidance and associated documents on plagiarism: https://documents.manchester.ac.uk/display.aspx?DocID=2870
In order that your report conforms to the standards for a technical report, you should use the following structure:
• Typeset using LaTeX, so the only allowed submission filetype is pdf, and it must be submitted without your name, but with your university ID number online through the TurnItIn system.
• approximately 8 - 10 pages long (excluding appendices)
• be written in continuous prose
• give a brief introduction stating the problem you are solving and the parameters you are using (from the model or method),
• present your results in the form of figures and tables, using the order of items in the bullet points as a guide as to the order of your document
• absolutely NO screenshots of running code need to be included,
• do not include overly long tables – a table should never cross over a page,
• present the results for any methods you have implemented, there is no credit for a discussion of a method that has not been shown to be implemented by you (through results) for your problem
• refer to and discuss each of your results in the text, part of the marks available in each bullet point are for interpreting the results
• try to keep to the page limit, removing any unnecessary results from the main text
• number and caption your figures and tables and refer to them by their number (not their position in the text),
• number any equations to which you refer,
• use consistent internal (and external) referencing.
RUBRIC
This assignment will account for 40% of your final mark in this module. The total number of marks in this assessment is 40, and they will be awarded as follows:
(i) 5 for working codes;
Grade Description
0-50% Little or no attempt, codes not working
50%-70% One or two bugs in the code are a↵ecting the results
70%-100% The results in 2.1 and 2.2 from the codes appear correct
(ii) 5 for the presentation of your written report;
Grade Description
0-50% Poorly presented work. Significant amount of text unreferenced. Graphs and tables poorly labelled making it difficult to interpret them.
50%-70% Good presentation. Text is readable. Graphs are ok, maybe miss-ing labels and not always referenced correctly. Report is overly long and unnecessarily repeats the same (or similar) results.
70%-100% Excellent presentation, well written and well referenced. Graphs are clear, tables used when appropriate. Report keeps within the page limit.
(iii) 20 for the understanding of the problems involved;
Grade Description
0-50% Results are poorly presented or they are without supporting text. The methods are described but are not shown to be implemented through results. The student is unable to demonstrate they can correctly interpret results.
50%-70% Demonstrates a good understanding of the standard methods. Is able to generate standard results and discuss them. Results are well presented.
70%-100% Student is able to correctly interpret standard results and evaluate the efficiency of the standard methods.
(iv) 10 for originality/initiative.
Grade Description
0-50% Little or no attempt at implementing any of the new methods. Those that have been implemented have poorly presented results or the student is unable to demonstrate they can correctly inter-pret results.
50%-70% Demonstrates a good understanding of new or alternative meth-ods. Is able to implement new methods, present results and dis-cuss them. Results are well presented.
70%-100% Has implemented difficult algorithms not detailed in the course. Presentation of the results is excellent. Student is able to correctly interpret results and compare methods in a coherent way.
See individual bullet points in the task section for a break down of the marks.