COMP9334 Capacity Planning of Computer Systems and Networks
Assignment (Version 1.02), Term 1, 2024
Due 5:00pm, Fri 15 March 2024 (Friday Week 5)
Change log and version info
Updates, changes and clarifications will appear in this box.
• Version 1.02 issued on 3 March 2024. Text (in magenta) added to Question to improve clarity.
• Version 1.01 issued on 29 February 2024. Text (in red) added to Question 1c to improve clarity.
• Version 1.00 issued on 26 February 2024
Instructions
(1) There are 3 questions in this assignment. Answer all questions.
(2) The total mark for this assignment is 20 marks.
(3) The submission deadline is 5:00pm Friday 15 March 2024. Submissions made after the deadline will incur a penalty of 5% per day. Late submissions will only be accepted until 5:00pm Wednesday 20 March 2024, after which no submissions will be accepted.
(4) In answering the questions, it is important for you to show your intermediate steps and state what arguments you have made to obtain the results. You need to note that both the intermediate steps and the arguments carry marks. Please note that we are not just interested in whether you can get the final numerical answer right, we are more inter-ested to find out whether you understand the subject matter. We do that by looking at your intermediate steps and the arguments that you have made to obtain the answer. Thus, if you can show us the perfect intermediate steps and the in-between arguments but get the numerical values wrong for some reason, we will still award you marks for having understood the subject matter.
You can take a look at the solution to revision problems to get some ideas the level of explanation that is required.
(5) If you use any computer programs to perform any part of your work, you must submit these programs or you lose marks for the steps.
(6) This is an individual assignment.
(7) Your submission should consist of:
(a) A report describing the solution to the problems. This report can be typewritten or a scan of handwritten pages. This report must be in pdf format and must be named report.pdf. The submission system will only accept the name report.pdf.
(b) One or more computer programs if you use them to solve the problems numerically. You should use zip to archive all the computer programs into one file with the name supp.zip. The submission system will only accept this name. The report must refer to the programs so that we know which program is used for which part.
(8) Submission can be made via the course website. Your submission must not be more than 20 Mbytes in size; otherwise it will not be accepted.
(9) You can submit as many times as you wish before the deadline. A later submission will over-write the earlier one. We will only mark the last submission that you make.
(10) If you want to ask questions on the assignment, you can attend a consultation (see the Timetable section of the course website for dates and times) or post your question on the forum. Please note that if your forum post shows part of your solution or code, you must mark that forum post private.
(11) Additional assignment conditions:
• Joint work is not permitted on this assignment.
– This is an individual assignment. The work you submit must be entirely your own work: submission of work even partly written by any other person is not permitted.
– Do not request help from anyone other than the teaching staff of COMP9344.
– Do not post your assignment work or code to the course forum.
– Assignment submissions are routinely examined both automatically and man-ually for work written by others.
Rationale: this assignment is designed to develop the individual skills needed to solve problems. Using work/code written by, or taken from, other people will stop you learning these skills. Other CSE courses focus on skills needed for working in a team.
• The use of generative AI tools, such as ChatGPT, is not permitted on this assign-ment.
Rationale: this assignment is designed to develop your understanding of basic con-cepts. Using AI tools will stop you learning these fundamental concepts, which will significantly impact your ability to complete future courses. Moreover, ChatGPT has been found to give incorrect answers for advanced problems covered in this course.
• Sharing, publishing, or distributing your assignment work is not permitted.
– Do not provide or show your assignment work to any other person, other than the teaching staff of COMP9334. For example, do not message your work to friends.
– Do not publish your assignment code via the Internet. For example, do not place your assignment in a public GitHub repository.
Rationale: by publishing or sharing your work, you are facilitating other students using your work. If other students find your assignment work and submit part or all of it as their own work, you may become involved in an academic integrity investigation.
• Sharing, publishing, or distributing your assignment work after the completion of COMP9334 is not permitted.
– For example, do not place your assignment in a public GitHub repository after this offering of COMP9334 is over.
Rationale: COMP9334 may reuse assignment themes covering similar concepts and content. If students in future terms find your assignment work and submit part or all of it as their own work, you may become involved in an academic integrity investigation.
(12) You are allowed to use or modify the sample code provided by the lecturer for your work in this assignment. You should acknowledge that in your report.
Question 1 (6 marks)
Assuming that you are the administrator of an interactive computer system. The computer system consists of a 2-core CPU and a disk. During an observation time of 1800 seconds, you obtained the following measurements from the system:
Busy time of Core 1 1015 s
Busy time of Core 2 1532 s
Disk busy time 987 s
Number of requests completed by the computer system 67
This computer system is used by 19 interactive users and the thinking time per interactive user is 45 seconds.
Answer the following questions.
(a) Determine the average service demand of Core 1.
(b) Determine the throughput upper bound on this interactive computer system.
(c) From reading the measurements above, you realise that the utilisations of the 2 cores are very different. You want to make an attempt to balance the utilisations of the 2 cores. In the ideal scenario, what is the lowest throughput upper bound (on the interactive system) that you can get from balancing the utilisation of the 2 cores?
You can assume that both cores have the same processing rate. For simplicity, you may assume that each request in this system is processed only by one core, i.e., no parallel processing. A request can be processed by any of the two cores. You can attempt to balance the utilisation of two cores by deciding on how the requests should be allocated to the cores.
(d) Part (c) considers the ideal scenario. Discuss one practical difficulty that can prevent you from perfectly balancing the utilisations of the 2 cores.
Reminder: If you use a computer program to derive your numerical answers, you must include your computer program in your submission. Do not forget to show us your steps to obtain your answer.
Question 2 (6 marks)
A call centre has 2 trainees to deal with customer enquires. The centre has a dispatcher to direct the calls automatically to one of the trainees. The dispatcher does not contain any queueing facilities. At each trainee’s terminal, there is a facility to queue up to 3 calls. The queueing network at the call centre is depicted in Figure 1.
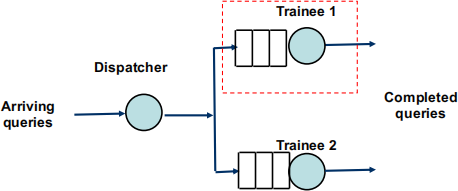
Figure 1: Depiction of the call centre.
The centre receives on average λ queries per hour. The arrivals can be modelled by using the Poisson distribution.
When a query arrives at the dispatcher, it will send the query to Trainee 1 with a prob-ability of p and to Trainee 2 with a probability of 1 − p. Note that the dispatcher does not communicate with the trainee’s terminals, so it is possible that the dispatcher sends a query to a terminal that has a full queue. You can assume that the dispatcher takes a negligible time to perform its work and no queries will be dropped at the dispatcher.
Nominally, Trainee 1 can complete or service on average µ1 queries per hour. This service rate applies when the number of customers waiting in their queue is 2 or less. However, when there are 3 customers waiting in the queue, Trainee 1 feels the pressure of the full queue and their service rate slows down to ν1µ1 where ν1 < 1. Trainee 2 performs in exactly the same way except that their service rate is µ2 and their service rate when their queue is full is ν2µ2 where ν2 < 1. You can assume all the service times are exponentially distributed and independent of each other.
When a query arrives at a staff’s terminal, it will be answered straight away if the staff is not busy. Otherwise, the terminal will place the call in its queue if the queue is not full. If a call arrives when the queue is full, then the call is rejected.
Answer the following questions:
(a) Formulate a continuous-time Markov chain for the part of the call centre consisting of Trainee 1 and their 3 waiting slots, i.e. the part enclosed by the red dashed lines in Figure 1. Your formulation should include the definition of the states and the transition rates between states. The transition rates should be expressed in terms p, λ, µ1 and ν1.
(b) Write down the balance equations for the continuous-time Markov chain that you have formulated.
(c) Derive the expressions for the steady state probabilities of the continuous-time Markov chain that you have formulated.
(d) Assuming that p = 0.45, λ = 5.3 and µ1 = 3.9 and ν1 = 0.86, determine the probability that a call which is dispatched to Trainee 1 will be rejected.
(e) Assuming that p = 0.45, λ = 5.3, µ1 = 3.9, ν1 = 0.86, µ2 = 3.5 and ν2 = 0.8, determine the mean waiting time of the queries that have not been rejected by the call centre. Note that Part (d) considers only queries that have been dispatched to Trainee 1 but Part (e) considers the whole call centre.
Hint:
• There is a mistake that some people may make regarding the calculation of the mean waiting time in Part (e). We will not tell you exactly what the mistake is but the following example of probability calculations will illustrate that. Let us assumed that you have two coins, which we will refer to as Coin 1 and Coin 2. Coin 1 is a fair coin and the mean number of heads you get is 0.5. Coin 2 is a biased coin and the mean number of heads you can get is 0.6. Let us say you do the following:
– You randomly pick one of the two coins with the probabilities of picking Coins 1 and 2 being, respectively, 0.7 and 0.3. You toss the coin picked. You repeat this many times.
You want to calculate the mean number of heads that you will get. A wrong answer is 0.55. The correct answer should be 0.53. △△△
Reminder: If you use a computer program to derive your numerical answers, you must include your computer program in your submission. Do not forget to show us your steps to obtain your answer.
Question 3 (8 marks)
This question considers a system with two processing units. There are two types of requests that can arrive at this system:
• The Type 1 requests require only one processing unit. These requests arrive according to a Poisson distribution with a mean rate of λ1. These requests require a processing time which is exponentially distributed with a mean processing time of µ1/1.
• Each Type 2 request requires two processing units simultaneously. By “simultane-ously”, we mean that a Type 2 request can only be admitted into the two processing units when both processing units are available. If admitted, both processing units will start to work on the admitted request at the same time and they will complete the request at the same time.
Type 2 requests arrive at the system according to a Poisson distribution with a mean rate of λ2. The above description says that a Type 2 request requires the same amount of processing time at each processing unit. The processing time required by a Type 2 request at each processing unit is exponentially distributed with a mean processing time of µ2/1.
The four inter-arrival and service time distributions are assumed to be independent.
The system has two queueing slots. One slot is reserved for Type 1 requests only and it has a capacity to hold exactly one Type 1 request. The other slot can only be used to hold Type 2 requests and it has a capacity to hold exactly one Type 2 request.
We first specify what happens when a request (either Type 1 or Type 2) departs the system upon its service completion. This departure can result in the availability of one or two processing units. We assume that the system gives a non-preemptive priority to the Type 1 request. The rules here are:
• If the Type 1 queueing slot is empty and there is a request at the Type 2 queueing slot, then the Type 2 request is admitted to the processing units if both units are available; otherwise, the request remains in the Type 2 queueing slot.
• If there is a request in the Type 1 queueing slot, then this request will be admitted into a newly available processing unit.
Note that the second rule above covers the case when both Type 1 and Type 2 queueing slots have a request each. In that case, the request in Type 1 queueing slot will be admitted because the second rule above gives the priority to the Type 1 request. Note also that the Type 2 request in the queue will not be admitted because there will not be two processing units available; the Type 2 request will remain in the queue.
Note that the above rules imply that:
• If there is a Type 1 request is in the queue, then it is not possible to have any idle processing unit.
• If there is a Type 2 request in the queue, then it is not possible to have two idle processing units.
• It is possible to have an empty Type 1 queue, an occupied Type 2 queue and one idle processing unit.
We now describe what happens when a Type 1 request arrives. These are the possible scenarios:
• If the Type 1 queueing slot is occupied, then this request is rejected.
• If the Type 1 queueing slot is not occupied, then:
– If at least one processing unit is idle, then this request will be admitted to an idle processing unit and its processing will begin.
– If both processing units are occupied, then this request will be admitted into the Type 1 queueing slot.
Finally, we describe what happens when a Type 2 request arrives. These are the possible scenarios:
• If the Type 2 queueing slot is occupied, then this request is rejected.
• If the Type 2 queueing slot is not occupied, then:
– If both processing units are idle, then this request will be admitted to both pro-cessing units and its processing will begin.
– If at least one processing unit is occupied, then this request will be admitted into the Type 2 queueing slot.
We will now use an example to illustrate the operation of the system.
Figures 2 and 3 illustrate how the state of the system changes over time for a given sequence of arrivals and departures. The state of the system consists of the following attributes:
• The status of the 2 processing units which are depicted as circles. There are 2 possible statuses for each processing unit: idle or busy. In Figures 2 and 3, a white circle is used to denote an idle processing unit while circles of other colours are used to denote busy processing units.
• The status of the Type 1 and Type 2 queues. Each queue has 2 possible states: empty or occupied.
We now go through each time point in Figure 2.
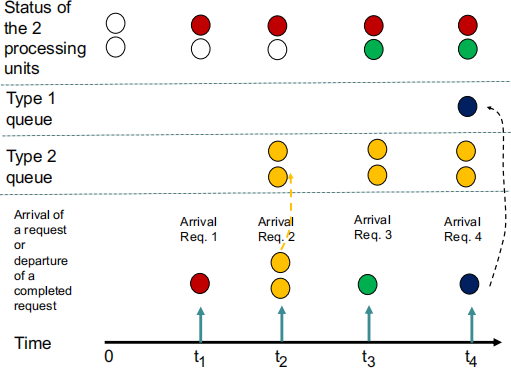
Figure 2: Example for Question 3 (Part 1)
At time 0, the system is assumed to have idle processing units and empty queues. At time t1, Request 1 (Red), which is of Type 1, arrives. Since both processing units are idle, the request goes to a processing unit. So one processing unit is busy (with the red request) and the other is idle.
At time t2, Request 2 (Orange), which is of Type 2, arrives. Since one processing unit is occupied and the Type 2 queue is empty, the request goes to Type 2 queue.
At time t3, Request 3 (Green), which is of Type 1, arrives. Since one processing unit is idle, this request goes to the idle processing unit.
At time t4, Request 4 (Black), which is of Type 1, arrives. Since both processing units are busy and the Type 1 queue is empty, this request goes to Type 1 queue.
This example continues on the next page.
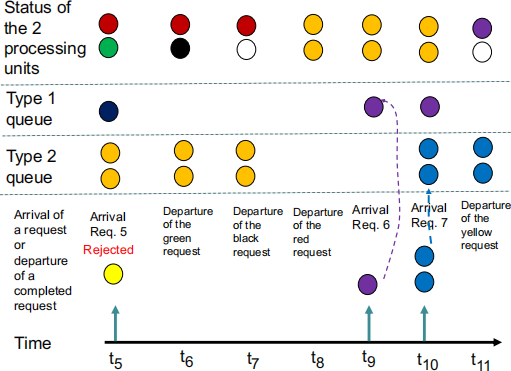
Figure 3: Example for Question 3 (Part 1)
At time t5, Request 5 (Yellow), which is of Type 1, arrives. Since both processing units are busy and the Type 1 queue is busy, this request is rejected.
At time t6, the green request in the processing unit has completed and departed from the processing unit. Since there is a request (black) in the Type 1 queue, this request is admitted into the processing unit that has become available.
At time t7, the black request in the processing unit has departed. The Type 1 queue is empty and Type 2 queue has a request. However, since only one processing unit is available, so the Type 2 request remains in the queue.
At time t8, the red request in the processing unit has departed. The Type 1 queue is empty and Type 2 queue has a request. Since both processing units are available, the Type 2 request is moved to the processing units.
At time t9, Request 6 (Magenta), which is of Type 1, arrives. Since both processing units are busy and the Type 1 queue is empty, this request goes to the Type 1 queue.
At time t10, Request 7 (Blue), which is of Type 2, arrives. Since both processing units are busy and the Type 2 queue is empty, the request goes to the Type 2 queue.
At time t11, the Type 2 (orange) request has completed its service. The departure of this request means that both processing units are now available. Since both Type 1 and Type 2 queues have a request each, the magenta request in the Type 1 queue is admitted to the server.
Answer the following questions:
(a) Formulate a continuous-time Markov chain for the system using the following 4-tuple as the state:
(number of Type 1 requests in the processing units,
number of Type 2 requests in the processing units,
number of requests in the Type 1 queueing slot,
number of requests in the Type 2 queueing slot).
Your formulation should include a list of all possible states and the transition rates between states. The transition rates should be expressed in terms λ1, λ2, µ1 and µ2.
Hint: Here are two examples of impossible states. The first is (1,2,0,0) because there are only 2 processing units, so it is not possible to have one Type 1 request and one Type 2 request in the processing units. The second is (1,0,1,0) because it is not allowed to have a Type 1 request in the queue while only one Type 1 request is being processed, i.e., there is an idle processing unit.
(b) Assuming that λ1 = 0.9, λ2 = 0.2, µ1 = 2.4 and µ2 = 0.8. All these four parameters have the unit of number of queries per some given unit time.
(i) Determine the steady state probabilities of the state of the continuous-time Markov chain that you have specified in Part (a).
(ii) Determine the probability that an arriving Type 2 request will be rejected.
(iii) Determine the mean waiting time of Type 2 requests.
Reminder: If you use a computer program to derive your numerical answers, you must include your computer program in your submission. Do not forget to show us your steps to obtain your answer.