CSCI 5512: Artiicial Intelligence II
(Spring 2024)
Exam 1
(Due Thu, Feb. 29, 11:59 PM CT)
Exam Policy. This is a take-home exam. Please explain your answers clearly. You will not get credit unless your explanation is correct. You are allowed to use the class books, lecture notes, and lecture videos. You are not allowed to discuss the exam with anyone else. Regarding online resources, you are not allowed to:
❼ Google around for solutions to exam problems,
❼ Ask for help online,
❼ Look up things/post on sites like Quora, StackExchange, etc.
❼ Use AI tools like ChatGPT
1. (10 points) Figure 1 shows a Bayesian network (without the conditional probability tables).
(a) (5 points) What is the relationship between P (B) and P (BjD) (i.e., are they equal or not)? Why?
(b) (5 points) Is B conditionally independent of D given C? (i.e., B ? DjC?)
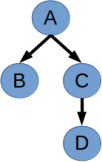
Figure 1: Bayesian network for Problem 1.
2. (20 points) Figure 2 shows another Bayesian network. Use variable elimination to ind P (a, :cjd). Note, you must ind the exact probability (you cannot leave it in terms of some value times α).
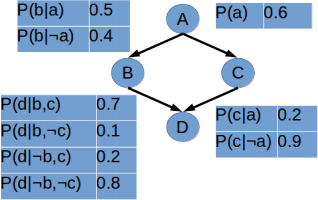
Figure 2: Bayesian network for Problem 2.
3. (18 points) Consider sampling-based inference for the Hidden Markov Model (HMM) in Figure 3 where Zt are unobservable state variables and Xt are observable evidence variables.
(a) (6 points) Describe the rejection sampling algorithm. Would you use rejection sampling for the given HMM, why or why not?
(b) (6 points) Consider likelihood weighting-based inference for the given HMM. Assuming X1:3 = {T, T, T}, what is the weight on the following two samples Z![]()
![]() = {F, F, F} and Z
= {F, F, F} and Z![]()
![]() = {T, T, T}?
= {T, T, T}?
(c) (6 points) Describe the particle iltering algorithm, clearly discussing the three steps involved. Would you use particle iltering for the given HMM, why or why not?
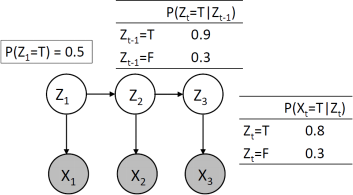
Figure 3: Hidden Markov Model for Problem 3.
4. (20 points) Suppose you are trying to make some quick cash by ishing. It costs ✩45 to rent a boat and ishing supplies. The number of ish you will catch is a random variable which has a discrete uniform distribution with support {5, 6, . . . , 15}. Each ish caught can be sold for $4. You can also purchase a guidebook that has a 25% chance of doubling the amount of ish you catch. How much should you pay for this guidebook (i.e., up to how many dollars would you be willing to pay)?
5. (5 points) Explain the explore-exploit tradeof. Why do we have this tradeof in RL?
6. (12 points) Write down the equation for cumulative regret in multi-armed bandits. Describe each part of the equation. What is the agent competing against? For a good bandit algorithm, what type of function should the cumulative regret be bounded by? Why?
7. (15 points) Using Figure 4, write down the arm selection equations for E-greedy and UCB. Using the igure below where ˆ(μ)i , ci, and -ci are the estimated reward, upper conidence bound, and lower conidence bound of arm i respectively, write down the probability that arm i = f1, 2, 3g is selected by E-greedy and UCB. (You should have 6 probabilities, one for each arm and algorithm. For E-greedy, leave the probabilities in terms of E.)
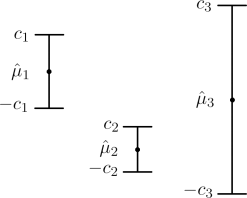
Figure 4: Estimated rewards and conidence intervals for Problem 7.
Extra Credit. In order for extra credit solutions to be considered, you must provide reasonable solutions to all parts above. If you skip any part of a problem or do not provide a reasonable solution (i.e., make a real efort), we will not count any extra credit towards your grade.
1. Extra Credit (5 points) This question considers the value of perfect information (VPI) V PIE(Ej) which evaluates the value of additional information Ej given existing information E. Prove that VPI is non-negative,i.e., V PIE(Ej) ≥ 0, Aj, E. (Your proof must be rigorous.)