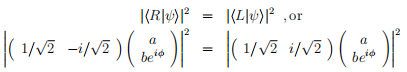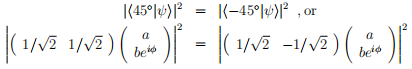Hello, if you have any need, please feel free to consult us, this is my wechat: wx91due
PHY256F: Problem Set #1
Assigned 11 September 2024
Due 11:59pm, Mon 23 Sep 2024 (to be submitted on Quercus)
1. Write down two different 2x2 matrices, each of which has the eigenvalues 0 and 2. It should be easy to find a purely diagonal matrix of this sort; you are to find at least one such matrix which is not purely diagonal, however.
Write down their corresponding eigenvectors.
Calculate the square of each of these matrices; find the eigenvectors and eigenvalues for these two new matrices.
2.
(a) A HeNe laser has a wavelength of 633 nm. Work out the energy of a single photon from this laser, in Joules.
(b) Calculate that energy in electron Volts.
(c) I shine a 5 mW laser beam from a HeNe laser on a piece of paper. The spot on the paper has an area of 4 mm2
, and I leave the laser on for 10 seconds.
How much energy has hit the paper, in Joules?
How many photons have hit the paper?
3. McIntyre Problem 1.2
4. An arbitrary polarization state of a photon may be written |ψ⟩ = α|H⟩+β|V ⟩ ≡ α
β
!
.
Since an overall phase has no measurable effect, we can take α = a and β = beiϕ, where a, b, and ϕ (and hence α) are all real.
(a) Suppose that the probability PR of this photon being transmitted by a right-circular polarizer is equal to the probability PL of it being transmitted by a left-circular polarizer:
What can you conclude about a, b, and ϕ? (Note that there is more than one way
to satisfy this condition.)
1(b) Suppose additionally that the probability P45 of this photon being transmitted by
a 45◦ polarizer is equal to the probability P−45 of it being transmitted by a −45◦
polarizer:
What more can you conclude about a, b, and ϕ?
(c) What can you say about the polarization of the photon?
5. McIntyre 1.6-a and 1.6-b
6. I have atoms in an unknown spin state, which we can write in complete generality as |ψ⟩ = a| ↑⟩ + b| ↓⟩.
Suppose that when I send them through a Stern-Gerlach analyzer along z, I find that 64% of them go up and 36% of them go down.
(a) What can you conclude about a and b (remembering that they are in general complex numbers)?
(b) Suppose this same state ψ were sent through an x-analyzer. Write down the probability for them to be deflected in each direction in terms of a and b. What are the maximum and minimum possible values for P(±x), the probabilities of being deflected along ±x?
(c) Suppose only the 64% that went up are sent through this x-analyzer – what can you say about P(±x)?
(d) Suppose only the 36% that went down are sent through the x-analyzer – what can you say about P(±x)?
(e) Redo the calculations of parts a and b above for a case where 50% of the atoms go up and 50% go down.