ST449 Assignment 1 (Autumn Term 2023)
Submission instructions
Answer all the questions below and submit your solution in two files (see below) via the Moodle submission link.
a. Please upload a .pdf document (max 3 pages) containing your answers to questions 1 and 2. Please name this document as ‘ST449_Assignment_XXXXX.pdf’, where ‘XXXXX’ is your 5-digit candidate number. The document can either be typeset or handwritten. If you choose the latter, please write legibly, otherwise you put yourself at a disadvantage.
b. Please upload a single python file ( .py ) for question 3. You should name this file as ‘ST449_Player_XXXXX.py’, where ‘XXXXX’ is again your 5-digit candidate number.
Your name must NOT appear anywhere in these two files. You can find your 5-digit candidate number on LSE for You. Note that this is NOT your student number.
Deadline for Moodle submission is 5pm on 24 November 2023. Late submission will incur penalties: 5 marks will be deducted for every half-day (12 hours). This will result in a maximum penalty of 10
marks for the first 24 hours. Then further 5 marks will be deducted per 24 hour period thereafter. Submissions after 5pm on 3 December 2023 will not be accepted.
The work you submit is expected to be 100% your own and you must not collaborate or confer with anyone during the assessment; see LSE Regulations on Assessment Offences
(https://info.lse.ac.uk/Staff/Divisions/Academic-Registrars-Division/Teaching-Quality-Assurance-and- Review-Office/Assets/Documents/Calendar/RegulationsAssessmentOffences-Plagiarism.pdf) for
more details. Please also read through the Student Guidelines on the Use of Generative Artificial
Intelligence (AI) Tools (https://moodle.lse.ac.uk/mod/resource/view.php?id=1212168) for this course. Submitting answers and code essentially generated by generative AI tools is an act of academic
misconduct and will result in 0 mark.
Questions
1. Your friend Lucy recently received a new puzzle “Lights Out”. The puzzle consists of 3x3 grid
of lights. When the game starts, all of the 9 lights are switched on. Pressing any light will toggle it and its adjacent (edge-sharing) lights from on to off and vice versa. The following picture
shows what happens when the centre light is pressed in the puzzle.
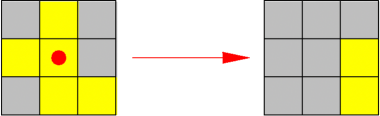
The goal of the puzzle is to switch all the lights off, preferrably with as few button presses as possible. After playing with the puzzle for a while, Lucy came to you to ask if your knowledge in AI could help her solve the puzzle quickly.
Your first thought is to use breadth-first graph search or A* search to find a solution.
i. What is the state space in this problem? What are the initial state and the goal state? ii. Write down the set of actions and the transition model.
iii. Assume that a solution to the puzzle exists. Is breadth-first graph search guaranteed to provide an optimal solution (in terms of the number of button presses)? Why? Does
breadth-first tree search work for this problem?
iv. You decided to use the number of lights switched on in a state as your heursitic function for A* search. Briefly describe how the heuristic function will be used to determine the
order in which nodes are expanded in an A* search and specify one data structure that can be used to arrange this order.
v. Is the heuristic function in part (iv) admissible? Explain.
After playing with this puzzle a bit longer, Lucy realised that if a solution exists, then every light on the board needs to be pressed at most once and that the order in which the lights are
pressed do not matter. This prompted you to model the puzzle as a constraint satisfaction problem (CSP).
vi. What are the set of variables, set of domains and set of constraints in this CSP?
vii. What is the constraint hypergraph in this problem? You can either describe the hypergraph in words or draw the hypergraph.
viii. You have an off-the-shelf CSP solver that can solve any CSP problem with binary
constraints. Explain how you can transform the original CSP problem into a form that you can feed into this solver. Use some example cases to help with your description.
2. Suppose a new viral infection, called Coronix, is discovered to hit on average 10% of the population. Luckily, a laboratory has come up with a test that detects Coronix with a false positive rate of 1% (i.e., out of 100 people not having Coronix, 1 tests positive) and a false negative rate of 2% (i.e., out of 100 people having Coronix, 2 test negative).
i. Suppose you test positive at the test. What is the probability that you have contracted Coronix? Detail your computation.
Consider the following Bayes net which describes the relation between Coronix, the seasonal flu and their symptoms.
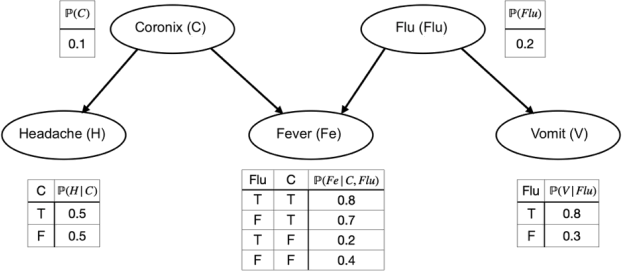
ii. Suppose you know you do not have Coronix. If you happen to have an headache, would this information affect the probability of developing a fever? Explain.
iii. Determine the probability
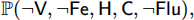
and provide detailed reasoning.
3. In this task, you are asked to submit a piece of python code that can play the following variation of the children’s game “Chopsticks” .
Rules of the game: The game is played by two players in turns. At the start of the game, each player stick out one finger in each of their two hands. A hand is called “busted” if all fingers are folded. In each turn, a player can choose one of the following actions:
![]() Tap: use one of her unbusted hand to tap on either one of opponent’s unbusted hand or her own other unbusted hand. Suppose the hand that initiate the action had x fingers sticking out and the hand that was tapped had y fingers sticking out, after the action,
Tap: use one of her unbusted hand to tap on either one of opponent’s unbusted hand or her own other unbusted hand. Suppose the hand that initiate the action had x fingers sticking out and the hand that was tapped had y fingers sticking out, after the action,
the tapped hand will need to stick out x + y fingers if x + y ≤ 5. If x + y > 5 , then
the tapped hand is considered “busted” and all its fingers should be folded.
![]() Split: Use one of her unbusted hand that has x ≥ 4 fingers sticking out to tap her own other busted hand. After this action, the originally unbusted hand has「x/2] fingers sticking out and the originally busted hand becomes unbusted and sticks out Lx/2」
Split: Use one of her unbusted hand that has x ≥ 4 fingers sticking out to tap her own other busted hand. After this action, the originally unbusted hand has「x/2] fingers sticking out and the originally busted hand becomes unbusted and sticks out Lx/2」
fingers.
A player wins a game by busting both of their opponent’s hands.
We will illustrate the rules with a few game plays. As children are confused about left and right, let’s call their hands A and B for player 1 and C and D for player 2. Player 1’s action can be
recorded as a two-character string from {AB, AC, AD, BA, BC, BD} , where the first letter denotes the tapping hand and the second letter the tapped hand (whether the action is a tap or a split can be inferred from the busting status of the tapped hand). We can use an 8-character alphanumeral string to denote the current state of the game. For instance, A2B3C1D0
means that player 1 has 2 fingers sticking out in hand A, 3 fingers in hand B, player 2 has 1
finger sticking out in hand C and hand D is busted (we record 0 fingers for a busted hand). The initial state of the game is A1B1C1D1. Here are some examples of legal moves by player 1 from various states.

In the last example, player 1 wins the game by busting both of player 2’s hands.
Your task: You can treat yourself as player 1. Please write a python script
( ST449_Player_XXXXX.py , where XXXXX is your 5-digit candidate number) containing a
function generate_move() that takes in as input the current state of the game (in the format of AxBgCzDw , where x, g, z, w = {0, 1, 2, 3, 4, 5} and outputs a legal move from the set {AB, AC, AD, BA, BC, BD} .
![]() Please submit only one .py file for this question.
Please submit only one .py file for this question.
![]() Your python script may contain other auxiliary functions, but please keep them in the same file.
Your python script may contain other auxiliary functions, but please keep them in the same file.
![]() You may assume that the Artificial Intelligence: A Modern Approach book package [https://github.com/aimacode/aima-python/archive/master.zip
You may assume that the Artificial Intelligence: A Modern Approach book package [https://github.com/aimacode/aima-python/archive/master.zip
(https://github.com/aimacode/aima-python/archive/master.zip)] is directly importable
from the working directory. For instance, you can use any classes/functions in games4e.py using from games4e import * .
![]() Use of the above AIMA package or object-oriented programming is not necessary. You
Use of the above AIMA package or object-oriented programming is not necessary. You
will not be disadvantaged for either using or not using them in your submitted code.
![]() You are not allowed to submit pre-computed results in a separate file. Any pre-
You are not allowed to submit pre-computed results in a separate file. Any pre-
computation, if required, needs to be carried out when your function is first called.
![]() Your function is allows to generate and use global variables. However, to prevent your code from producing errors due to global variable name conflicts, please prefix them with your 5-digit candidate number, i.e. in the form of _XXXXX_varname .
Your function is allows to generate and use global variables. However, to prevent your code from producing errors due to global variable name conflicts, please prefix them with your 5-digit candidate number, i.e. in the form of _XXXXX_varname .
![]() Please make sure that your function produces an output within the time limit described in the marking criteria below.
Please make sure that your function produces an output within the time limit described in the marking criteria below.
![]() Please check that your code runs properly using code_check.ipynb
Please check that your code runs properly using code_check.ipynb
(https://moodle.lse.ac.uk/pluginfile.php/2583354/mod_folder/content/0/code_check.ipynb?
forcedownload=1). Upload your code to the ./players/ folder in your working directory and run all code blocks in the notebook.
Marking criteria
The entire assignment has 100 marks, distributed as follows:

Your score for Q3 will be determined as follows. The first 10 marks will be awarded based on the
readability of the code you have submitted, measured in terms of clarity of writing, structure of the
code and usefulness of comments. The remaining 40 marks will be awarded through a double round- robin tournament, where your submitted code will play against every other submitted code twice
(taking turns to play first). In each match:
![]() The match is played for a maximum of 50 rounds (i.e. each player making 50 moves) and a draw is declared if neither player wins at the end of 50 rounds.
The match is played for a maximum of 50 rounds (i.e. each player making 50 moves) and a draw is declared if neither player wins at the end of 50 rounds.
![]() Each player has a total of 5s in each match (for a maximum of 50 moves). So you should aim to generate each move within 0.1 second. If your cumulative time exceeds 5s in a match, all subsequent moves will be generated at random. Code timing is done on a desktop machine with 8 cores, each at 2.9GHz. This time limit should be much more than enough.
Each player has a total of 5s in each match (for a maximum of 50 moves). So you should aim to generate each move within 0.1 second. If your cumulative time exceeds 5s in a match, all subsequent moves will be generated at random. Code timing is done on a desktop machine with 8 cores, each at 2.9GHz. This time limit should be much more than enough.
![]() You lose a match if your code generates an error during the match. Note in particular that this includes generating illegal moves, e.g. tapping with a busted hand. Please check that your
You lose a match if your code generates an error during the match. Note in particular that this includes generating illegal moves, e.g. tapping with a busted hand. Please check that your
code runs properly using the code_check.ipynb notebook before submission.
In addition to submitted code from the class, three simple bots ( random_bot.py
(https://moodle.lse.ac.uk/pluginfile.php/2583354/mod_folder/content/0/players/random_bot.py? forcedownload=1), defensive_bot.py
(https://moodle.lse.ac.uk/pluginfile.php/2583354/mod_folder/content/0/players/defensive_bot.py? forcedownload=1), aggressive_bot.py
(https://moodle.lse.ac.uk/pluginfile.php/2583354/mod_folder/content/0/players/aggressive_bot.py?
forcedownload=1)) will also participate in the tournament. You can find the code for the three bots on Moodle. For each game, you get 2 points for a win, 1 point for a draw and 0 point for a loss. Suppose
you have S points after the tournament, and the best submission in class has M points and the three bots have B1 , B2 and B3 points respectively. Your final score (out of 40 marks) will be
decided by the following formula:
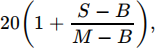
where B = (B1 + B2 + B3 )/3 is the average of bot points. In other words, the best submission has full mark and the pass mark for this part is set at the average bot points.