MAT237 Multivariable Calculus with Proofs
Problem Set 7
Due Thursday March 14, 2024 by 23:59 ET
Problems
1. Show that the figure eight curve C = {(sin t, sin t cost) ∈ R 2 : 0 ≤ t ≤ 2π} is a piecewise curve.
2. Fix 0 < r < R. Let A and B be the counterclockwise oriented circles centered at the origin with radius r and R respectively. Let F : R2 \ {(0, 0)} → R2 be a C1 vector field. Assume F is irrotational.
Do not use Green’s theorem for any part of this question.
(2a) (Revised 2024-03-06) Fix 0 < α < π. Parametrize the α-keyhole contour K along part of the circles A and B as the concatenation of four curves γ1 ,γ2 ,γ3 , and γ4 as shown in this figure. No justification necessary.
(2b) Explain why  Hint: Consider F on a restricted domain U ⊆ R2 containing K.
Hint: Consider F on a restricted domain U ⊆ R2 containing K.
(2c) Prove that 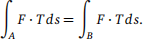 Hint: Relate γ1 and γ3 to two small arcs of A and B.
Hint: Relate γ1 and γ3 to two small arcs of A and B.
3. Let F = (f , g) be a vector field in R 2 with C1 components f and g. Fix a point p = (x, y) ∈ R2.
For ε > 0, let Rε(p) = {(x + s, y + t) : (s, t) ∈ [−ε, ε] 2 be the square centered at p with sidelengths 2ε.
Orient its boundary ∂ Rε(p)counterclockwise. Do not use Green’s theorem for any part of this question.
(3a) For ε > 0, show that the circulation of F along ∂Rε(p) may be expressed as
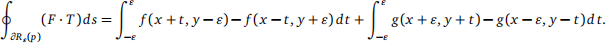
(3b) Since f is C1 on U, differentiability implies that there exists δf > 0 and Ef : Bδf (0, 0) → R such that ∀(∆x,∆y) ∈ Bδf (0, 0), f (x + ∆x, y + ∆y) = f (x, y) + ∂1 f (x, y)∆x + ∂2 f (x, y)∆y + Ef (∆x,∆y),
where 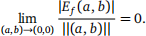 The analogous statement holds for g with δg > 0 and Eg : Bδg (0, 0) → R.
The analogous statement holds for g with δg > 0 and Eg : Bδg (0, 0) → R.
Prove that for 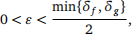
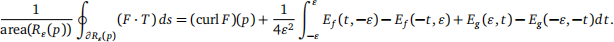
(3c) Use the definition of the limit to prove that 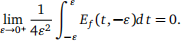 Assuming without proof that similar identities hold for Ef and Eg , conclude that curl is “circulation density”:
Assuming without proof that similar identities hold for Ef and Eg , conclude that curl is “circulation density”:
