BACHELOR OF ENGINEERING
FACULTY OF ENGINEERING
ENGG1300: FUNDAMENTAL MECHANICS
Homework Assignment 4 (Dynamics)
Show intermediate steps for each question, instead of only providing a final answer.
1. (40 marks) A bomb (JDAM) is released at t=0 with an initial velocity along the horizontal direction, vb = 200 m/s. A anti-aircraft system (LD-2000) fires immediately to intercept the bomb. The projectiles (from the gun) have an initial speed (muzzle velocity) of va = 1,000 m/s. The distance between the bomb and the anti-aircraft gun is shown in the graph. Neglect aerodynamic effects.
(1) Determine the angle θ for the projectiles that allows successful interception. (2) Identify the time t’ and the heighth at which the projectiles hit the bomb.

P.S. This problem is designed solely for the practice of kinematics priciples and is never intended to promote violence or military conflict. Indeed, in the given scenario, nobody will be injured regardless of the involvement of weapons.
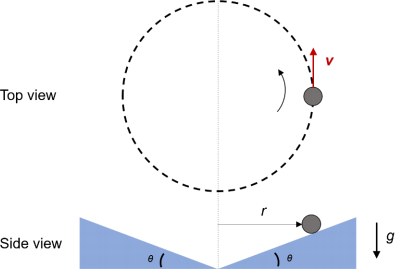
2. (30 marks) A particle with a mass of m is doing a circular motion with a constant speed of v on an inclined smooth surface (neglect friction). The radius of the circle is r. Derive the inclination angle θ, which allows the particle to maintain this uniform circular motion.
3. (20 marks) A COMAC C919 airliner has a total mass of about 60,000 kg. During a takeoff, its CFM LEAP engines are ejecting massive amount of air with very high velocity. The total air mass flow rate at its engines is 960 kg/s. The exhaust velocity of the air is 280 m/s. Estimate the total thrust and the acceleration of the C919 when it starts to take off. Show your reasoning as well.

4. (3 marks) Suggest a reference coordinate system for each of the following applications. You can refer to the Cartesian/normal & tangential/polar coordinates that we discussed in the class. Please also explain why you make your choices.
(1) A 3D bioprinter has three translation axes perpendicular to each other. You are programming this 3D bioprinter to fabricate a tissue scaffold for regenerative medicine.

(2) Tracking airplanes at the control tower of the Hong Kong international airport.

(3) Analyzing the dynamics of race cars driving on the track of Indy 500.

5. (2 marks) A rigid disk is rotating with a constant angular velocity of ω. There is a smooth groove on the disk that allows free motion of a particle along the radial direction of the disk. At t=0, a particle with a mass m is placed in the groove with a distance to the center of r0. The particle has no initial velocity along the radial direction. No need to consider gravity. Determine the following parameters as a function of time t (t>0):
(1) The radial velocity of the particle. (Hint: recall 2nd order ODE)
(2) The lateral force acting on the particle, which is exerted by the wall of the groove.

6. (3 marks) Particles A and B are moving rectilinearly along the same line. At some point, they collide with each other. Their masses and velocities before the collision are shown in the graph. Assume no external force or mass exchange. Determine:
(1) The velocity of the center of mass (G) of the system consisting of A and B, and the velocities of A and B in the center-of-mass frame of reference before the collision.
(2) The linear momentum and the kinetic energy associated with G before and after the collision.
(3) The total kinetic energy of the system (EK ), and the kinetic energy of the system relative to its center of mass (EKG ), before the collision.
(4) EK and EKG after the collision if e = 0, 0.5 or 1.
(5) The maximum velocity particle B can have after the collision. (Specify the frame of reference you use)

7. (2 marks) A cylindrical rigid body with a radius of r is released from rest aty=0. It rolls downhill without slipping. Its moment of inertia about its central axis G is IG = 1/2mr2. At y=h, determine the magnitude of its angular momentum about G.
