Hello, if you have any need, please feel free to consult us, this is my wechat: wx91due
DEPARTMENT OF ECONOMICS
ECON0001
ECONOMICS OF FINANCIAL MARKETS
Formative assessment n.2 on the first part of the unit
Section A: investment under risk or uncertainty (30 marks)
1. [Total 10 points] Consider the decision problem of investing an amount of wealth W = £1000000 into a risky asset with return
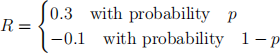
and into a risk-less asset with risk-free interest rate r = 5%. You are a risk averse investor with a CRRA utility function
where ρ = 2, and WT is the amount of wealth at the end of the investment.
(a) How do you set up the solution of the optimal allocation problem of the two assets?
(b) Find the optimal allocation in risky and risk-less assets as a function of the probability p and the initial amount of wealth W invested. How does it depend on p? Comment on your result.
(c) Compute the optimal allocation for a probability value p = 1/2.
(d) What is the lower bound of the probability p for investing a positive share into the risky asset? Try answering this question with and without using the utility function, and compare, arguing about the role of risk aversion.
(e) How do you find the lower bound of the probability p for starting to borrow money at the risk-less interest rate and invest an amount larger than W in the risky asset?
(f) Find this lower bound of probability.
2. [Total 10 points] Consider a risky asset with return expressed by
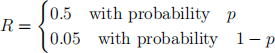
and a utility function U(WT ) = ln(WT ), where WT is the final value from investing wealth W.
(a) Why does this utility imply a risk premium for the given investment? What are the assumptions on the probability distribution of the risky asset?
(b) Find the Certainty Equivalent of the investment for such utility as a function of the probability p of the higher return value and the invested wealth W. How does it depend on p? Comment on your results.
(c) Compute Certainty Equivalent and Risk Premium for a probability p = 50%.
(d) How does the risk premium depend on the probability p? How can you check if the risk premium is a non-monotonic function of the probability p?
(e) What is the risk premium for p = 0 and for p = 1? Comment on your results.
(f) Find the probability p that maximises the risk premium (for this it may be useful to know that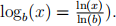 
3. [Total 10 points] An investor with utility function
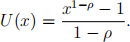
faces the decision problem of allocating her wealth of £100000 in the following assets: a risky asset that gives a return of 20% or a loss of −4% with equal probability, and a risk-less asset with interest rate equal to 5%.
(a) What is the rational for an optimal investment allocation that is based on expected utility?
(b) How do you expect the optimal allocation to depend on risk aversion ρ? Find the optimal shares invested in risky and risk-less asset as a function of ρ. Check your answer in the limit ρ → ∞ and ρ → 0, and comment on your result.
(c) What is the condition on risk aversion ρ for the optimal allocation to be 100% invested in the risk-less asset? Justify your answer both conceptually and mathematically.
(d) What is the condition on risk aversion ρ for the optimal allocation to be 100% invested in the risky asset? For this condition it may be useful to know that 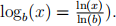Comment on your answer.
(e) Evaluate the marginal effect of ρ on the optimal investment share of the risky asset. Is this marginal effect increasing or decreasing with ρ? You can answer with a general mathematical result, or checking how the optimal investment share of the risky asset changes from ρ = 1 to ρ = 2 and from ρ = 2 to ρ = 3.