Economics 101 - Spring 2021
MIDTERM 2, Version 1
This midterm has a total of 20 questions. All of them have the same weight (about 4.55 percent of the total score), except for two items which are worth double (they’re clearly marked below). Items 1 through 9 are short, individual questions. Items 10-13 are two short question split into two parts each. Items 14 through 20 correspond to two long questions.
Short questions (items 1 through 13)
1. Suppose we want to sustain cooperation in a situation where both economic agents have short-run incentives to unilaterally deviate, but because they expect the situation to occur again in the future, they might beneit from cooperating. Think of this situation as analogous to the ininitely repeated prisoner’s dilemma. Which of the following statements is INCORRECT (if any)?
(a) The less the agents care about the future, the harder it is to sustain cooperation.
(b) The higher the perceived probability of interaction being repeated, the easier it is to sustain cooperation.
(c) The higher the interest rate, the easier it is to sustain cooperation.
(d) The harder it is to detect a deviation, the harder it is to sustain cooperation.
(e) None of the statements above are incorrect.
2. What is the most important source ofirst-mover advantage in the Stackelberg compe- tition model seen in lecture, where irms choose quantities sequentially?
(a) The irst mover is the irst to announce their desired quantity.
(b) The irst mover is better informed about the market.
(c) The irst mover has an advantage in cost.
(d) The irst mover is able to commit to their chosen quantity regardless of what the second irm does.
(e) The second mover can commit to a credible threat against the irst mover’s strat- egy.
3. Which of the following statements on dynamic games is INCORRECT?
(a) Players moving irst in a sequential game do not necessarily have better payofs.
(b) In a two-stage game with two players, if the second mover does not observe the irstmover’s action, then the equilibrium result is the same as if the game is played simultaneously.
(c) In a two-stage game, changing the order in which players execute their actions is likely to change the equilibrium result.
(d) If a strategy proile is not a SPNE in one particular subgame, then it is not a SPNE for the entire game.
(e) The result of backward induction is not necessarily a subgame perfect Nash equi- librium, even in inite sequential games with perfect information.
4. Consider an ininitely repeated, symmetric Prisoner’s Dilemma game with two players. Which of the statements below is correct?
(a) Suppose that for some particular discount factor δ* , the “Grim Trigger” strategy proile is a subgame perfect Nash equilibrium (SPNE). If that assumption is true, then the same strategy proile is also a SPNE for any other discount factor smaller than δ* .
(b) If δ is too small, then a strategy proile where both players always play ”defect” (D) is not a SPNE.
(c) Suppose that the players have diferent discount factors: 0 < δ1 < δ2 < 1. Consider the Grim Trigger strategy proile. If player 2 does not have a proitable deviation (that is, playing the Grim Trigger is the best response to 1 playing the Grim Trigger), then player 1 does not have a proitable deviation as well.
(d) Assume that the “Perfect Tit-for-Tat” strategy is a SPNE if the discount factor is a speciic value δ* for both players. Then, both players adopting the “Grim Trigger” strategy is also a SPNE for the same discount factors δ* .
(e) None of the above is correct.
5. Which of the following statements about entry and competition is INCORRECT?
(a) It might be optimal for irms to use strategies that hurt their short-term proits in order to prevent entry of other irms, or to induce exit of competitors.
(b) Even with only one irm in the market, the equilibrium outcomes might notrelect the standard problem of the monopolist (discussed in the irst part of the course) if there is a credible threat of new entrants.
(c) It is impossible to fully understand competition in a market without understanding potential barriers to entry.
(d) Because of the ever-present threat of entry, real markets are almost always per- fectly competitive in the long run. The rare exceptions are utilities.
(e) All of the statements are correct.
6. Consider the following game:
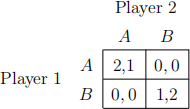
In the Nash equilibrium with (strict) mixed strategies, what is the probability that player 2 plays A?
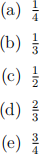
7. Consider an ininitely repeated game where, in each period, two irms compete a la Bertrand. The irms have identical cost curves C(q) = 2q and face market demand schedule given by Q(p) = 10 -p (since this is Bertrand, the p that matters is the lowest one). Firms are also identical in the discount factor δ 2 (0, 1). Suppose the irms try to collude. In order to avoid regulators, they choose a cartel price that is halfway between the monopoly price and the Bertrand Nash equilibrium price. Their agreed-upon strategy is to keep playing this cartel price unless any of them chooses a diferent price in any previous period. After any of them deviates from the cartel price, they switch to choosing price equal to marginal cost. What is the lowest level of the discount factor δ required for sustaining collusion?
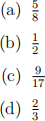
(e) There is not enough information to calculate the minimum δ.
8. Consider the following normal form game:

Consider the strategy proile: the row player plays U, M and D with probabilities 0.6, 0.2 and 0.2, respectively; the column player plays L with probability 0.8 and R with probability 0.2. Consider the list of values of (a,b,c, d) below. Which of them makes this strategy proile a Nash Equilibrium?
(a) a = 3, b = 2, c = 6, d = 0
(b) a = 3, b = 11, c = 9, d = 4
(c) a = 2, b = 2, c = 6, d = 0
(d) a = 2, b = 11, c = 9, d = 0
(e) a = 2, b = 2, c = 6, d = 4
9. In an ininitely repeated game, N identical irms (N ≥ 2 is inite) compete every period a la Bertrand. All irms have constant marginal costs c ≥ 0 and no ixed costs. The market demand is given by Q = a - bp, where a, b > 0. Firms are secretly considering a collusive strategy where they start by playing the monopoly price pm , and keep doing so until a deviation is detected. When it is, all irms switch permanently to playing price equal to marginal costs.
Which of the following statements is CORRECT?
(a) The larger the number of irms N , the easier it is to sustain the collusive agreement.
(b) If a decreases, i.e., market demand goes down, then it becomes harder to sustain the collusive agreement.
(c) If a price loor p 2 (c, pm ) is imposed, then is becomes harder to sustain the collusive agreement.
(d) If a price ceiling p 2 (c, pm ) is imposed, then it becomes easier to sustain the collusive agreement.
(e) None of the above is correct.
Information for questions 10 and 11: Consider a market where two irms compete a la Bertrand. Market demand is q(p) = 64 - p, and marginal cost of both irms is c = 60. Because of regulatory issues, irms are only allowed to set integer prices. For example, setting prices to 59, 60, or 61 is ok, but 60.5 or 60.99 are not allowed).
10. How many Nash equilibria does this game have? Hint: draw a matrix of payofs. You can ignore prices lower than 60 or higher than 62.
(a) 0
(b) 1
(c) 2
(d) 3
(e) An ininite number.
11. This question is worth double. Suppose that the game is repeated two times in a row, and payofs in the second round are discounted by δ 2 (0, 1]. Is it possible to sustain collusion in the irst round?
(a) No, because with a inite number of repetitions, the game ”unravels” and so players end up playing the Nash equilibrium of the stage game in every round.
(b) No, because it would require δ > 1.
(c) Yes, but only if δ = 1.
(d) Yes, but only if δ ≥ 1/2.
(e) Yes, but only if δ ≥ 2/3.
Information for questions 12 and 13: Consider a duopoly with two identical irms indexed by i 2 f1, 2g. The game is sequential. In the irst period, irm 1 commits to a quantity choice. Then, irm 2 chooses quantity. At the end of the game, prices are determined by the total quantity produced Q = q1 + q2 , according to the inverse demand p(Q) = 10 - Q. But diferently from the standard Stackelberg model, the cost function for both irms is:
C(q) = 2(q + q2 )
12. What is the best response of irm 2 to irm 1’s chosen quantity?
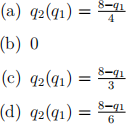
(e) None of the above.
13. What is the quantity chosen by irm 1 in a subgame perfect Nash equilibrium of the game?
(a) 20/17
(b) 0
(c) 40/17
(d) 4
(e) None of the above.
Long Question 1 (items 14-16)
In the 2000’s, the Brazilian national government implemented an audit program to detect political corruption at the city level. After prominent political economists used econometrics to show that the program was successful, the government is deciding to do it again. To do so, they need to design the program and advertise it, incurring in some ixed costs F. On top of that, for each city that the government decides to inspect, it must pay additional costs c, corresponding to training inspectors, paying for their wages during the inspection, and travel costs.
In each city, the mayor may choose to steal or not. If the mayor steals and there is no inspection, he gets a beneit of B, which corresponds to a loss of the same magnitude from the point of view of the national government. If the mayor steals and there is a inspection in the city, the mayor does not get the beneit B: it is forced to pay back the money to the government. On top of that, the mayor gets a negative payof -P corresponding to the punishment for corruption. Assume that P > B > c > 0.
14. Consider the payofs for the mayor and the national government corresponding to cor- ruption in one particular city, in the scenario where the government has recreated the program and may choose to send an inspector to the city. What matrix below represents these payofs correctly?
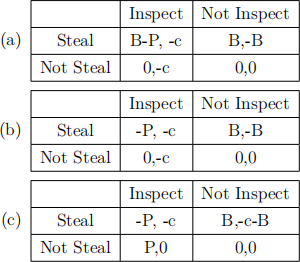
(d) It is not possible to represent the payofs in a matrix.
(e) None of the options above is correct.
15. This question is worth double. Now model this problem as a sequential game, where the players are the national government and a number N of mayors. In the irst stage, the government decides to fund the program or not, paying ixed cost F. The mayors observe whether the program is funded or not. In the second period, each of the mayors decides to steal or not. If the government decides to fund the program, in the second stage they may choose to inspect each particular city or not. The inspection and stealing decisions are simultaneous. If the government does not fund the program, then it cannot inspect any city.
Think about the subgame perfect Nash equilibrium(a) of this game, allowing for mixed strategies. Which of the following statements is accurate?
(a) The government will fund the program only if (B - c)N ≥ F.
(b) It is irrational for mayors to engage in corruption if the government funds the program.
(c) There is no subgame perfect Nash equilibrium for this game.
(d) It is never optimal for the government to fund the program.
(e) The equilibrium level of corruption decreases with the punishment P.
16. Now consider a modiied sequential game. In the irst stage, the government decides whether to fund the program. In the second stage, it commits to a probability of au- diting each city. Speciically, the government announces the probability to the public, and years later (when it’s time for the audits), they conduct a public lottery live on TV that determines which cities will be audited. In the third stage, after knowing the probability of auction but before knowing if their particular city will be audited, the mayors decide whether to steal or not.
Thinking about the diferences between this game and the one from the previous ques- tion, which of the following statements is correct?
(a) There is a subgame perfect Nash equilibrium in which some mayors engage in corruption.
(b) There is a subgame perfect Nash equilibrium with zero corruption, but the ex- pected payof for the government is smaller than in the game from the previous question.
(c) There is no subgame perfect Nash equilibrium.
(d) Knowing the probabilities with certainty improves the expected outcomes of may- ors, compared to the previous game where the probabilities and stealing where decided simultaneously.
(e) There is a subgame perfect Nash equilibrium with zero corruption, and the ex- pected payof for the government is larger than in the game from the previous question.
Long Question 2 (items 17-20)
Consider the following game. In the irst stage, the Government decides whether to implement intellectual property rights (IPR) regulations or not. In the second stage, an Innovator irm observes the IP choice of the government and decides whether to innovate or not, paying a ixed cost FI to do so. Innovating means creating a new product, for which the inverse market demand is given by p(Q) = a - bQ. The marginal cost of the product is a constant c. What happens after depends on the Government and Innovator actions:
❼ If the Innovator irm chooses not to innovate, the game ends with payof zero to all players.
❼ If the Innovator irm innovates and the government chooses to implement IPR regula- tions, then the Innovator operates in the newly created market as a monopolist.
❼ If the Innovator irm innovates and the government has not implemented IPR regu- lations, then another player, the Follower irm, is allowed to copy the technology at some ixed cost FC . If the follower pays that cost, it can produce the goods at the same marginal cost c, and irms compete by choosing quantities simultaneously a la Cournot. If the follower does not pay the copy ixed cost, it does not enter the market and the Innovator operates as a monopolist.
The payof of the government is assumed to be the consumer surplus. For all items in this long question, assume that a > c > 0, b > 0, and FI > FC > 0.
17. Consider the subgame after the government decides NOT to implement IPR regulations. In that subgame, can there be a subgame perfect Nash equilibrium where the Innovator irm chooses to innovate? Hint: draw the game tree and calculate formulas for the payofs for both frms (but skip the government) .
(a) Yes, always (given the assumptions on parameters made above).
(b) No; because FC < FI , the Follower irm will always end up better of than the innovator without IPR, and thus the Innovator has no incentives to innovate.
(c) Yes; all that is needed is that FI is small enough.
(d) Yes; but it requires not only a low FI but also a su伍ciently high FC .
(e) No; prices will be set equal to marginal cost at the last stage, and thus choosing to innovate always leads to negative payofs due to the ixed cost.
18. Continue to focus on the subgame without IPR. Suppose that the game is modiied in the following way: after the Innovator decides to Innovate, the Innovator has a new action: it is allowed to choose an illegal payment X 0 to the Follower, along with a request to not enter the market in return for the payment. After the payment and message are received by the Follower, the Follower chooses to enter or not as before. Which of these statements is correct?
(a) Because payment is received before the decision to enter, it does not afect the Follower’s incentives, and thus equilibrium payments will always be zero.
(b) Under some circumstances, the Innovator may choose a payment X equal to the payof the Follower if it entered the market, as a way of reducing the competition and seizing monopolist policies.
(c) The payment is not socially optimal because it would be better to have the Inno- vator irm innovate, but then the Follower produce since FC < FI .
(d) The Innovator will never use the payment because an X that was large enough to induce the Follower to not enter would hurt the Innovator more than the efect of competition itself.
(e) None of the statements above is correct.
19. What is the efect of IPR on consumer surplus? Your answer should be based on the comparison of the SPNE in the two subgames following the Government choice: with IPR and without IPR. Hint: since we are looking for a “qualitative” answer, not quantitative, you don’t need to go crazy with the math.
(a) It is always negative, because it gives monopoly power to the Innovator and thus generates deadweight loss.
(b) In general, we should expect the efects to be negative. While there is a theoretical possibility of a positive result, in the real world this would be extremely rare.
(c) It might be positive or negative depending on the parameters; sometimes IP can induce innovation where it wouldn’t exist, but sometimes it will decrease compe- tition where there would be innovation anyway.
(d) It is always positive, because it stimulates innovation, and without innovation the consumer surplus is zero (since there is no market in that case).
(e) It might be positive or negative depending not on the market parameters, but on the duration of the monopoly rights granted by IPR.
20. Consider another modiication of the game. Now, in the subgame with no IPR, com- petition is sequential. After the decision to innovate, the Innovator irm is allowed to commit to quantity choices. After observing the quantity posted by the Innovator, the follower decides whether to enter or not, and if so, what is the quantity produced. Then, the equilibrium price and payofs are determined. Which of these statements is accurate?
(a) The outcome of the game is identical to the case with Cournot competition.
(b) The sequential nature of competition makes it more likely that there will be in- novation, but consumer surplus might not always increase since the Follower irm might be driven out of the market.
(c) The sequential nature of competition makes it less likely that there will be inno- vation, since the Follower irm has an informational advantage over the Innovator.
(d) The change in the game shifts payofs for the second irm, but it has no efect on the innovation decision.
(e) The sequential nature of competition makes it more likely that there will be in- novation, and consumer surplus surely increases since Stackelberg quantities are larger than Cournot quantities.