Hello, if you have any need, please feel free to consult us, this is my wechat: wx91due
MAST20029 Engineering Mathematics, Semester 1 2024
Assignment 1
Submit a single pdf file of your assignment on the MAST20029 website before 9am on Monday 25th March.
• This assignment is worth 5% of your final MAST20029 mark.
• Assignments must be neatly handwritten, but this includes digitally handwritten documents using an ipad or a tablet and stylus, which have then been saved as a pdf.
• Full working must be shown in your analytical solutions.
• All sketches should be drawn clearly with appropriate labelling.
• All final answers should be in an exact form; decimal approximations will not be accepted.
• You must use methods taught in MAST20029 to solve the assignment questions.
• For the MATLAB questions, include a printout of all MATLAB code and outputs. This must be printed from within MATLAB, or must be a screen shot showing your work and the MATLAB Command window heading. You must include your name and student number in a comment in your code.
1. Let V be the solid region that is bounded below by the xy-plane, on the sides by the sphere
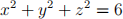
and above by the cone
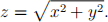
The mass per unit volume of V is
(a) Sketch V. Clearly label any intercepts and points of intersection.
(b) Determine the mass of V using spherical coordinates.
(c) Check your answer to part (b) using the MATLAB symbolic toolbox.
2. Let C be the part of the curve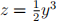 
in the plane x = 1 from (1, 2, 4) to (1, 0, 0). Consider a cable in the shape of C with mass per unit length
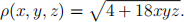
(a) Write down a parametrisation for C in terms of an increasing parameter t.
(b) Use MATLAB to sketch C in R3.
(c) Determine the mass of the cable.
3. A greenhouse has a glass dome in the shape of the paraboloid
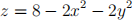
and a flat wooden floor at z = 0. Let S be the closed surface formed by the dome and the floor, oriented with outward unit normal.
Suppose that the temperature in the greenhouse is given by
The temperature gives rise to a heat flux density field
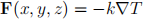
where k is a positive constant that depends on the insulating properties of the medium. Assume that k = 1 on the glass dome and k = 3 on the wooden floor of the greenhouse.
(a) Sketch S, clearly labelling any intercepts and the direction of the normal vector.
(b) Write down an expression in terms of x, y and z for the vector field F on the greenhouse.
(c) By direct calculation (do not use any integral theorems), find the total heat flux
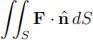
across the greenhouse in the direction of the outward unit normal.