MATH2545: Financial Mathematics: Markets
Assignment 1
This assignment contributes 10% of your overall module mark. It has 5 questions, each ques-tion is worth 20 marks.
Your solutions to these problems must be your own work and usage of any AI is prohibited (code Red). You risk losing all credit for the assignment if this is not the case. You must include your name, your student ID and the module code on your script. You must also complete an academic integrity form and upload this with your solutions. The deadline for this assignment is 4pm Thursday 29 February 2024. Scripts must be submitted via the Submit my Work area of the Assessment and Feedback folder on Minerva. Late submission after the deadline will be accepted until 4pm Monday 4 March, but late submissions will be penalised by 25 marks. Late submissions after 4pm Monday 4 March 2024 will not be marked at all.
Once marking is complete, it is your responsibility to check for your mark on Minerva. You must do this as soon as possible after marks are released.
1. (i) A utility function has the form U(w) = aw3+bw2 where a, b ∈ R. Assuming w > 0 and a ≠ 0, is U(w) ever suitable for a non-satiated and risk-averse investor? If it is, state the range of values of w this holds for as a function of a and b. You must include your working.
(ii) Give an example of a utility function with DARA. Show all your working.
(iii) An investor has IRRA. Would this investor prefer a fair gamble or to do nothing? Provide a short explanation of your answer.
2. Alice believes that her car would cost ↔12500 to replace if it was stolen or damaged. Based on crime statistics for the area she lives in, she believes that the probability of her car being stolen or damaged is 0.15.
(i) Alice’s utility function is given by U(w) = ln(w) for w > 0 and she as ↔35000 in the bank. Calculate how much Alice would be prepared to pay (in a single payment) to insure her car against theft or damage
(ii) Repeat the calculation in the previous part but now assume Alice has ↔500000 in the bank.
3. A market consists of two risky assets and no risk-free asset. Let R1 and R2 denote the return on each of the risky assets. Using market data the following have been estimated: E[R1] = 0.10, E[R2] = 0.15, σ2 1 = V ar(R1) = 0.1 2 , σ2 2 = V ar(R2) = 0.2 2 and ρ1,2 = − 2/1 where ρ1,2 denotes the correlation coefficient for R1 and R2.
(i) Given that an investor is targeting a total expected return of µ = 0.125 on a portfolio, what is the minimum variance that can be achieved?
(ii) Determine the global minimum variance portfolio and the expected return and variance of return on this portfolio.MATH2545: Financial Mathematics: Markets
(iii) Using your answers to parts (i) and (ii) make a rough sketch of the minimum-variance set in µ − σ 2 space. You should indicate the efficient frontier and the global minimum variance portfolio.
(iv) Without further calculation, explain how you would expect the variance of return calculated in (ii) to change if the two risky assets were independent.
4. Assume that a risk-free money market account is added to the market described in Q3. The continuously compounded rate of return on the money market account is 0% per period.
(i) Use the method of Lagrange multipliers to determine the proportions of wealth invested in the three assets available for the minimum variance portfolio with expected return µ. Your answer must express the proportions as a function of µ.
(ii) Recall that the market portfolio has highest Sharpe ratio. Formulate the optimi-sation problem which characterises the market portfolio. You don’t have to solve this optimisation problem.
5. Suppose we have a risky asset with random return R. We have defined R to be,
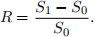
Now we introduce the log-return, which is defined as R = ln (S0/S1). In this question, assume that R ∼ N(µ, σ2 ) where µ = 0 and σ2 = 0.1.
(i) Show that R = e R − 1.
(ii) Calculate V aR0.95 for an investment of ↔150. Remember that if X ∼ N(µ, σ2 ) then eX is lognormally distributed with parameters µ and σ 2 . You may use that for a standard normal random variable Φ−1 (0.05) = −1.6449, where Φ denotes the CDF.