Problem Set 31
Physics 321
Electrodynamics I
Due on Wednesday, December 6th, 2023
Reading: for Monday, pp. 273–287 (skim to see the magnetization, auxiliary field, linear magnetic response story), plane waves in material setup: pp. 401–402.
Problem 1
a. For the potential and magnetic vector potential shown below (in Lorenz gauge), find E and B,

with ω = kc.
b. For the pair

again with ω = kc, find the relation between A0 and V0 that ensures Lorenz gauge. Find E and B. What is the polarization vector? What is the wavelength of the electromagnetic wave?
Problem 2
For the electric field in vacuum, E = E0 [cos(kz − ωt) ˆx + sin(kz − ωt)ˆy] with kc = ω. Find the associated magnetic field. Sketch the vector E in the xy plane at z = 0 (with the z axis pointing out of the page), and indicate its behavior as a function of time.
Problem 3
Two infinite sheets of charge are moving with constant speed – the top sheet moves at speed v to the right, the bottom moves with speed 1/2v to the left. Both sheets have the same constant surface charge σ, they are a distance d apart. Find the magnetic field in the three regions shown (above, between and below).
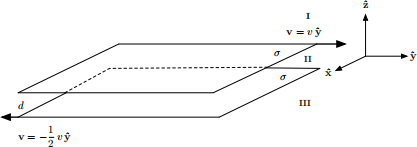
Figure 1: Two infinite sheets with constant surface charge σ moving in opposite directions separated by a distance d.
Problem 4
Find the magnetic field along the ˆz axis for a circular loop (radius R) of uniform line charge λ spinning at constant angular velocity ω.
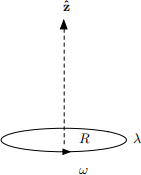
Figure 2: A loop of constant line charge λ rotates with constant angular velocity ω = ωˆz.