CSE546: Computational Geometry
Homework 2: Line intersections, planar subdivision, and triangulation
Due: before class on Tuesday, Feb 20, 2024
Reminder Unless otherwise stated, you may assume that input objects are in general position, and that any geometric primitive involving a constant number of objects each of constant complexity can be computed in O(1) time. Solutions to questions that ask for an algorithm need to present a pseudocode description of the algorithm, an analysis of the runtime, and an argument that the algorithm gives the correct output on all possible inputs.
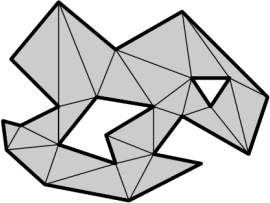
Question 1: In the lecture, we prove that any triangulation of a simple polygon with n vertices has exactly n − 2 triangles. Consider a non-simple polygon P with “holes” (see picture). Suppose that P has h ≥ 0 holes and n vertices in total (including those on the hole boundaries). Give an exact formula of the number of triangles in any triangulation of P, in terms of h and n, and prove its correctness.
Question 2: A polygonal chain in the plane is a sequence of vertices C = {v1, ..., vn}, where each consecutive pair (vi , vi+1) is connected by a line segment, called an edge. Such a chain is said to be X-monotone if any vertical line intersects the chain in a single point. A collection of chains is said to be independent if no two intersect each other (see figure).
Present an algorithm which, given a set of m X-monotone polygonal chains C = {C1, ..., Cm}, determines whether they are independent. (The algorithm does not need to report the intersections, just needs to indicate whether any intersection exists.) Let ni denote the number of vertices in the
i-th chain, and let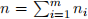 
be the total size of all the chains. Your algorithm should run in time O(n log m). (Thus if m is a constant, your algorithm should run in O(n) time.)
Question 3: Design an efficient algorithm that determines if a simple polygon is monotone with respect to some unknown direction. Recall that a polygon is l-monotone if there are no split or merge vertices when sweeping a line orthogonal to l over the polygon. Complete the following tasks:
1. Given a vertex v on the polygon with previous vertex v − and next vertex v + in CCW order, what is the range of directions of l in which v is not a split or merge vertex? We call this range the “safe range” of v.
2. Suppose the polygon has n vertices. Give an O(n log n) time algorithm that determines if the safe ranges of all vertices have a non-empty intersection.
There is actually an O(n) time algorithm for this problem, but is considerably harder. If you are interested, check out the paper “Testing a simple polygon for monotonicity” by Preparata and Supowit.