ECON705: Homework 4
Exercise 1. Take the model
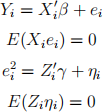
Assume there’s no perfect multicollinearity among variable Xi or Zi . Find the method of moments estimators (
, 
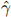for (β, γ)
Exercise 2. The observed data is {Yi , Xi , Zi}, Yi is 1×1,Xi is k×1,Zi is l×1, and l > k > 1, i=1,...,n. The model is Yi =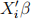 
+ ei with E(Ziei) = 0. Assume all the fourth moments of variables are finite.
a Given a weight matrix W > 0 write down the GMM estimator for β.
b Suppose the model is misspecified in question [b], [c] and [d]. Specifically, assume that for some δ ≠ 0,
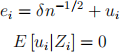
with µZ = E [Zi ] ≠ 0. Show that E(Ziei) ≠ 0.
c Express 
(− β) as a function of W, n, δ, and matrix format of the variables (Xi , Zi , ui)
d Find the asymptotic distribution of (− β). Assume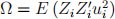 
and Ω > 0.
Exercise 3. Take the modle Yi = θ + ei with E(Xiei) = 0. And Yi is 1 × 1,Xi is k × 1. (Yi , Xi) ,i=1,..n, are iid across i.
a To write down the moment equation as E [gi (θ)] = 0, please write down gi (θ). What’s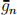 
(θ)?
b Is this model over-identified or just-identified?
c Given a weight matrix W > 0, write down the criterion function J (β) for the GMM estimator.
d Find the GMM estimator.
d Assume E (Xi) = µX,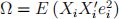 
and Ω > 0. Derive the asymptotic distribution of (
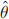− θ).
Exercise 4 Stata Application. Continuation of Exercise 4 in HW3, based on the empir-ical work reported in Acemoglu, Johnson and Robinson (2001).
The dataset is AJR2001 on the textbook website.The variables we are using in this exercise include loggdp, risk, logmort0.
a Re-estimate the model estimated in part (e) from HW3 by two-step efficient GMM under heteroskedastiticy assumption. Report the estimates and robust standard errors of the coefficients. Report the J statistic for overidentification and the conclusion about the test.
b Re-estimate the model in [a] by two-step efficient GMM under homoskedasticity as-sumption. What’s the test statistic for the overidentification test and what’s your conclusion about the test?
c Re-estimate the model in [a] by 2SLS. Are the estimates the same with those in [b]? Why?