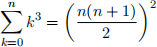CS1800 Discrete Structures
Fall 2023
Exam2 (Practice)
Due: do-not-submit
Instructions:
• HW instructions
• academic integrity and collaboration
Problem 1 Expected Value & Variance: Call Center Wait Times
An internet service provider’s call center receives calls which are each one of the following types:

Table 1: Probability of Response Time for Call Center (Sum to 1)
i Compute the expected time it takes to handle a single call
ii An employee working at the center is able to handle 15 calls in an hour (this employee’s calls follow the same distribution as above). Is this employee typically faster or slower than others in the group? Explain
iii Compute the variance in time it takes to handle a single call
Problem 2 When it rains, park wherever you’d like
A license plate reader is a system which identifies the text of a license plate given a camera’s image of the back of a car (useful in parking enforcement). When its not raining, the system is able to identify 99% of the license plates correctly. Unfortunately, when it rains the system struggles to see clearly and only identifies 90% of the license plates correctly. In a particularly rainy parking lot, there is a 1/4 chance of rain each day.
i What is the probability that its raining and a license isn’t read correctly?
ii What is the probability that its not raining and a license isn’t read correctly?
iii What is the probability that a license isn’t read correctly?
iv Suppose that you receive a parking ticket for someone else’s car because their license plate was incorrectly read as yours. What is the probability that it was raining when this other car’s license plate was read incorrectly?
Problem 3 Lottery Balls
In a lottery, 6 balls are drawn from a pool of 49 balls painted with numbers 1 through 49.
i What is the probability that the numbers on the chosen balls are all squares of integers (e.g. 1, 4, 9, ...)?
ii What’s the probability that all the six chosen numbers are composite (i.e. not prime)? (Since 1 is not considered prime, we will view 1 as a composite number for the purpose of this question).
Problem 4 Breadth / Depth First Search
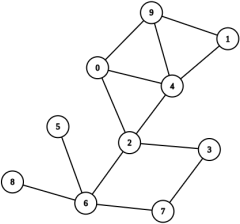
Give the order of nodes in each of the searches below, starting at the indicated node. When a method may select from among many next candidate nodes, prefer the node which has a larger value.
i Breadth First Search starting at node 2
ii Depth First Search starting at node 2
iii Breadth First Search starting at node 4
iv Depth First Search starting at node 4
Problem 5 Dijkstra’s Shortest Path
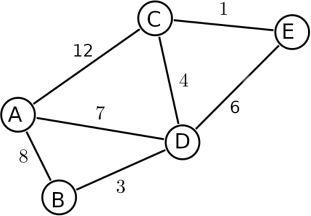
Using Dijkstra’s algorithm, find the total weight of the shortest path from node A to E. You do not need to give the path itself, only its total weight. To show your work, give the vector representing the “shortest path weight from A” as well as the list of nodes “visited” every step, formatted as:

Problem 6 HW1 Problem 6: Part II
Use induction to show that:
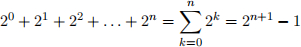
Problem 7 Function Growth (n! < nn )
Using induction, show that n! < nn for all n = 2, 3, 4, . . ..
Problem 8 K to the third power
Prove, using mathematical induction, that