Hello, if you have any need, please feel free to consult us, this is my wechat: wx91due
MATH 262
Financial Mathematics
Second semester 2023-2024
Exercises Sheet 6
Exercise 1
We consider the experiment of throwing once a dice (with six sides), then the set of possible outcomes (or scenarios) is Ω = {1, 2, 3, 4, 5, 6}, and P({ω}) = 6/1 for any ω ∈ Ω. Let X be the random variable that indicates the obtained number, i.e. X : Ω → R with X(ω) = ω for any ω ∈ Ω. Let A := {1, 3, 5}, i.e. the event that an odd number is obtained.
1. Calculate P(A).
2. Calculate P(X = 1), P(X = 2), and E[X].
3. We suppose that you don’t see the outcome of this experiment, but someone told you that the event A occurred, that is an odd number is obtained (but you don’t know which number preci-sely). Given this piece of information : What is the probability of the event that the obtained number is 1 ? What is the probability of the event that the obtained number is 2 ? What is the expected value of the obtained number ?
4. We suppose the following situation : you are sitting in your office room, and a dice is thrown once in another room. You don’t see the outcome of this experiment, but you are only allowed to know (from a friend of you) if either an even number is obtained or an odd number is obtained. Thus, the observable events for you (observable not with your eyes but in the sense that you know if those events occurred or not) are A and ¯A (often denoted by Ac). You would like to expect the value of X, so if the event A occurs, then the expected value of X in this case is E[X|A] ; if the event Ac occurs, then the expected value of X is this case is E[X|Ac]. Calculate E[X|A] and E[X|Ac].
5. Let F := {∅, A, ¯A, Ω}, the σ-algebra of observable events. Using the explanation and the results of the last question, how do you interpret the random variable E[X|F].
Exercise 2
We consider the random variable X representing the loss of an insurance company. X has the following discrete distribution
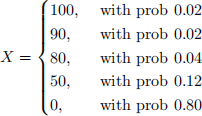
The conditional tail expectation (CTE) at probability level δ denoted by CTEδ(X) is defined as
CTEδ(X) = E[X|X > VaRδ(X)].
The tail Value-at-Risk, denoted by TVaRδ(X) is defined as
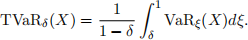
1. Compute CTE0.95(X).
2. Compute TVaR0.96(X) (Hint : remark that VaRξ(X) is equal to some constant if ξ ∈]0.96, 0.98], and is equal to another constant if ξ ∈]0.98, 1]).
Exercise 3
We fix a filtration (Fn)n∈I , I = {0, . . . , N}, let X be an adapted stochastic process.
1. Prove that X is a supermartingale if and only if −X is a submartingale.
2. Prove that X is a martingale if and only if (Xn − X0)n∈I is a martingale.
3. Prove that : If X is a martingale, then for m ≤ n one has
E[Xn|Fm] = Xm.
4. Prove that : If X is a martingale, then for any n ∈ I, E[Xn] = E[X0].