ECON12-200 Linear Models and Applied Econometrics

Homework 1:

Due in Week 5 by Friday 4pm

Learning Outcomes covered in this assessment:

1. Demonstrate knowledge of linear regression, its maintained assumptions and their relevant statistical properties.

2. Use  simple/multiple  regression  models  to  interpret  the  underlying  relationships between the variables and evaluate their statistical significance through hypothesis testing.

4. Demonstrate the ability to solve business problems using econometrics packages.

5. Demonstrate the ability to produce a written report that demonstrates higher order understanding of key concepts in applied econometrics.

Context

Regression analysis is a powerful statistical tool used in real life for various purposes, primarily to model and analyse relationships between variables.

Formatting

Assignment can be typed or hand-written or combinations of both. If it is hand-written, take an image and convert them into PDF. Homework assignments must be submitted in iLearn in a single PDF file.

Use of Artificial Intelligence

You can utilise GAI to assist with your questions However, you must adapt the AI- generated answers to conform with the methods taught in this course. Students maybe asked to explain their answers if they use a different approach from what is taught in class  in  order  to  receive  full  credit.  Be  sure  to  appropriately  reference  any  cited materials. Inappropriate use of subject content or other sources in your response will be considered a breach of the University’s academic integrity policy. Refer to the Bond University   Generative   Artificial   Intelligence   (GAI) resources for   guidance.   All assessments must include aStatement of Authorship.

Academic Integrity

Academic Integrity means adhering, in words and actions and across all aspects of student   life, to an academic moral code bound by Bond’s seven integrity principles of honesty, trust, fairness, respect, responsibility, courage, and professionalism. Breaches of academic integrity are known as either poor scholarship or academic misconduct. The University supports Academic Integrity by providing students with resources and support. Visit

Academic Integrity at Bondor seek support from your educators,BondCare support servicesincluding theAcademic Skills Centre, orLibrary services.

Rubrics

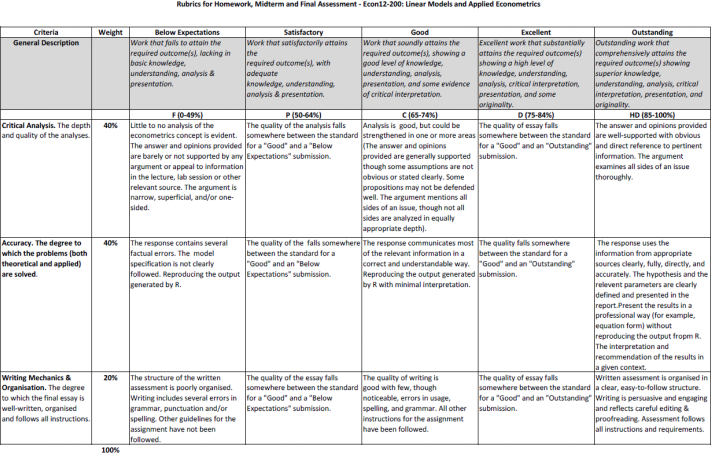
Case: Traffic congestion

Victoria’s transport system has three major problems. The first problem is congestion and crowding, with Victorians experiencing significant congestion on roads, trains and trams.

This means trips take longer, are less comfortable and less reliable, which costs people and businesses time and money. The second problem is that the accepted solution of building new infrastructure to ease congestion won’t solve congestion unless they take other steps. The third problem is that there are no incentives in the current system for people to change their   behaviour. Current pricing system is simple enough, but it doesn’t encourage people to make different choices about the time, route, mode or quality of their trip. This means that even as  congestion worsens, people are not motivated to change their behaviour.

In this case study, we observe the movement of Prof. Bill Griffith on each morning between 6.30AM and 8.00AM, who leaves the Melbourne suburb of Carnegie to drive to work at the University of Melbourne.  The time it takes Bill to drive to work (TIME) depends on the departure time (DEPART), the number of red lights that he encounters (REDS), and the number of trains that he has to wait for at the Murrumbeena level crossing (TRAINS). Observations on these variables for the 231 working days in 2006 appear in the file “Homework1.xlsx” . TIME is measured in minutes. DEPART is the number of minutes after 6.30AM that Bill departs.

You will assist Prof. Griffith to develop a model to predict the time it takes Bill to drive to work.

Question1

Professor observes the following based on the sample of 18 trips:

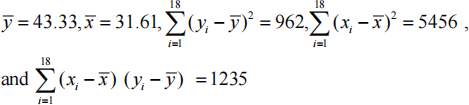
where y = the time it takes Bill to drive to work and x = departure time. Answer the following based on the summary information above 18 trips. Note: Do not use Excel file to answer Question1.

(a)  Compute the correlation coefficient between x andy.                           (4 Marks)

(b)  Compute the least squares estimates of β1  and β2  in the model: y = β1 + β2 x + e . Interpret the regression coefficients.    (8 Marks)