MAT 137Y: Calculus with proofs
Assignment 7
Due on Thursday, Mar 14 by 11:59pm via GradeScope
1. Determine if the following improper integral is convergent or divergent.
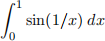
2. Definition: A miniature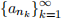 
of a sequence 
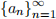is defined as {an1 , an2 , an3 , ...} where n1 < n2 < n3 < ....
(a) Given a sequence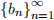 
with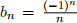 
, which of the following are miniatures of ?
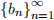Select All Apply.
(b) Here are two following theorems:
Theorem A: If a sequence of non-empty closed bounded intervals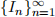 
with In = [an, bn] satisfies
I1 ⊇ I2 ⊇ I3 · · · ,
then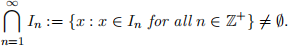 
Theorem B: Every sequence 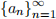has a convergent miniature.
Harsh thinks Theorem B is true, here is the proof of his argument:
Proof. 1. Consider any interval I1 := (−A, A) ⊆ R containing the sequence 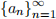, i.e. an ∈ I1 for any n ∈ Z+.
2. Split the interval into two halves U1 := (−A, 0) and V1 := (0, A)
3. Now at least one of U1 and V1 must contain infinitely many terms of 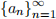, so with loss of generality let’s say that it is U1 and define I2 := U1
4. Now split I2 into two halves U2 and V2, and with loss of generality take I3 := U2 because one of U2 and V2 must have infinitely many terms of .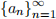
5. Iteratively repeat to create a sequence of non-empty intervals I1 ⊇ I2 ⊇ ...
6. Apply Theorem A so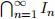 
is non-empty, let’s say it contains L
7. For each Ik, we can pick an increasing {nk} to get a miniature {ank } such that ank ∈ Ik for each k.
8. Since both L and ank are contained in each Ik, it follows that ank converges to L
Critique the above proof by answering the following questions.
(1) Why we can find a miniature {ank } such that ank ∈ Ik for each k in step 7? Rigorously justify this claim.
(2) Can you find a counter-example for Theorem B? Justify your answer.
(3) Although Theorem A is true, it turns out you need one more assumption to make Theorem B a true statement, identify what assumption to be added.
(4) Harsh’s reasoning has some flaws, identify the two steps which contain errors and give a brief justification as to why those lines have flaws.
(5) The end of Harsh’s proof, although correct, lacks justification when he claims ank converges to L. Rigorously justify this claim:
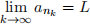
Hint: you may use the size of the intervals In in your proof.
3. (Refine Big Theorem) This problem aims to extend the list in the Big Theorem about sequences. We say n ∈ N = {1, 2, 3, · · · }.
(a) Show that ∀a < 0, 0 < b < 1,
bn << na << 1
(b) Construct a sequence un such that ∀a < 0, 0 < b < 1,
bn << un << na
and prove your claim. Hint: your un may depend on bn and na .
(c) Construct a sequence vn such that ∀M > 0, c > 0, a < 0
na << (vn)M << nc
and prove your claim.
4. Ces`aro summation is an alternative way to sum sequences.
Let 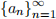be a sequence and 
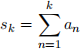an be its partial sum. The Ces`aro sum of {an}n is defined as
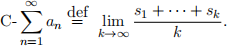
Determine if the following statements are true or false. If it is true, prove it directly. If it is false, provide a counterexample and justify it satisfies the required conditions.
(a) If a series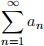 
is convergent, then its Ces`aro sum exists and it’s equal to .
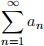True False
(b) If the Ces`aro sum of a series 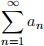exists, then 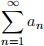is convergent to this sum.
True False