Hello, if you have any need, please feel free to consult us, this is my wechat: wx91due
ECON60662
ECONOMIC GROWTH
2019 – 20
SECTION A
1. The decision problem for an infinitely-lived agent is given as follows:
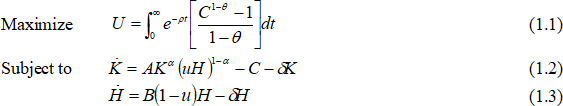
where (), C denotes consumption, K denotes physical capital, H denotes human capital, u denotes the fraction of human capital used in production, δ denotes depreciation of respective capital. The total population of agents is fixed and normalised to one.
(a) Solve the above problem to obtain the agent’s Euler equation. [7.5 marks]
(b) If , then find the expressions for in terms of χ, ω, and u. [5 marks]
2. In an infinitely lived agent economy, production function is given by:
and growth rates of capital and consumption are as follows:
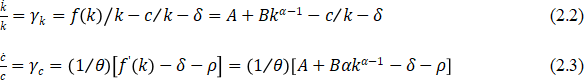
where (), 
denotes consumption per capita, 
denotes capital per capita, 
denotes depreciation of capital. The total population of agents is fixed and normalised to one.
(a) If , and , then find the expressions for 
and 
. [7 marks]
(b) Show the transitional dynamics through a phase diagram in (
) space, assuming . [5.5 marks]
3. In an infinitely-lived, representative agent model, the growth rates of consumption, 
, and capital, 
are given by
() where is a technology factor that grows at an exogenous rate, .
(a) Derive the following expressions for changes in growth rates.
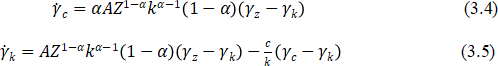
[6.5 marks]
(b) Consider a steady state equilibrium with positive growth in which . Verify that this equilibrium is characterised by (i) if , and (ii) if . [6 marks]
4. In an overlapping generations economy a two-period-lived agent born at time 
faces the following decision problem:
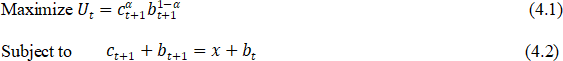
() where denotes consumption when old, denotes bequests to children ( being the inheritance from parents) and 
denotes other income.
(a) Solve the above problem to determine the optimal as a function of . [5.5 marks]
(b) Consider some critical value of – call it – and suppose that is dictated by the following criteria: agents for whom must work in subsistence, earning an income of ; agents for whom , can take on a project to earn an income of . Characterise, both algebraically and diagrammatically, the dynamics of wealth distribution. [7 marks]
5. The decision problem facing an infinitely-lived agent is given as follows:
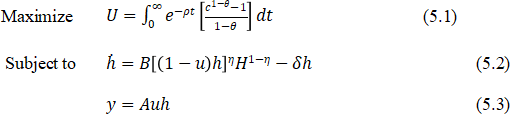
Where (), denotes consumption per capita, denotes output per capita, denotes human capital per capita and denotes aggregate human capital. The total population of agents, is constant and normalised to one. As there is no physical capital accumulation, where and are aggregate consumption and aggregate output respectively.
(a) Solve the above problem to obtain the Euler equation for consumption. [6 marks]
(b) Show that there is a unique equilibrium of u under balanced growth. [6.5 marks]
6. The decision problem facing an infinitely-lived agent is given as follows:
() where denotes consumption, denotes capital and denotes aggregate capital. The total population of agents is constant and normalised to one.
(a) Solve the above problem to obtain the Euler equation for consumption. [5.5 marks]
(b) What is the equilibrium growth rate of consumption? How does this compare with the growth rate that would be chosen by a central planner? [7 marks]
SECTION B
1. Outline the Ramsey model of growth with consumer optimization and explain the transitional dynamics with a phase diagram. Find the value for steady-state savings rate, and show that , where is assumed to be the elasticity of output with respect to capital. Explain the behaviour of savings rate during the transition period.
2. Develop a model of endogenous growth with distributive conflict among agents with varying capital-labour ratio to show:
(a) A government that maximizes the welfare of the representative individual cannot maximise the economy’s growth rate. [30 marks]
(b) Higher inequality in wealth under majority voting leads to lower growth. [20 marks]
3. Using a model of your choice, explain how public sector corruption can impede economic development, and why corruption and poverty may co-exist as persistent (rather than transitory) phenomena.